LSAT 29, Game 3 Setup, Awards, LSATHacks

LG Game 3 Setup, by LSATHacks

This is an explanation of the third logic game from Section III of LSAT Preptest 29, the October 1999 LSAT.

Seven language awards will be presented by a college dean. The awards are for research in French, German, Hebrew, Japanese, Korean, Latin and Swahili (F, G, H, J, K, L, S). The awards must be presented consecutively, only once, one at a time.

Game Setup

This game is a mix of linear and sequencing. By combining the rules, we can see that this game is very restricted.

The main diagram should have seven spaces. I’ve added the first rule: G can’t go first.

Here are the next two rules. H is before K, and L is before J.

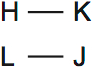
We can combine the fourth and fifth rules with these. F is beside H and K is beside L:

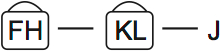
I’ll explain what this picture means. The box shows F and H go beside each other, and the handle on top shows that their order is reversible. Think of it like a suitcase handle — you can pick up the box and turn it around. 

So  means FH or HF. The same is true of KL. 

We know H is before K. So FH must be before KL. And KL is before J, since K is before J.

Simple, right? You can draw the whole game with one simple line. Just remember that G can’t go first, and S can go anywhere.

Hi, I'm Graeme Blake

Founder of LSAThacks; I scored a 177 on the LSAT.

I created the LSAT Mastery Seminars, which are part of the Ultimate LSAT Prep Bundle

If you like the explanations you're reading I'm 100% confident you'll enjoy the courses. Satisfaction guaranteed.

---------
Updates:

For updates, sign up for my email list. I update whenever I have new posts.