LSAT 29, Game 4 Setup, Piano Classes, LSATHacks

This is an explanation of the fourth logic game from Section III of LSAT Preptest 29, the October 1999 LSAT.

There are six piano classes to be held in a day. Nine students will attend these classes. There are four females – Gimena, Holly, Iyanna, and Kate (G, H, I, K) – and five males (M) – Leung, Nate, Oscar, Pedro, and Saul (L, N, O, P, S). Each of them will attend exactly one class. Two piano classes will have more than one students and four classes will have exactly one student.

Game Setup

This game is a mix of grouping and sequencing. We have to order the variables and say which of them go together in a group.

I draw games for speed and efficiency. I rarely find it useful to draw rules in the order they’re presented.

I start with simple rules, then focus on rules that can be combined with them.

It’s easiest to explain by example. The first rule is the simplest:

IL are a group. 

There’s nothing we can do with the second rule right away, so we should ignore it. 

K is the first female. That means she goes before IL (Iyanna is a female).

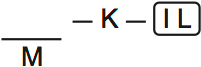
K is not the first student, so some male goes before her. We don’t know who.

The fourth rule lets us connect the second rule to the rest of the diagram. So now we can add the second rule. I try to draw things only once, if I can.

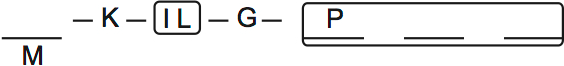
The fourth rule says that G comes after IL but before P. And the second rule tells us P is in a group with 2 other people. 

We can add a few other things. H must come after K, because K is the first girl. 

The last rule tells us that O is after G. 

Now, who can be the boy(s) that goes before K?
There are five boys: N, S, P, L, O. Everyone but N and S come after K. So the only boys that can go before K are N and S.

Make sense? We need at least one boy before K, and only N and S are free.

That diagram above is the main diagram. But we still have to figure out who can go with P. I’ll show you a few sample scenarios to clarify how this game works in practice. (next page)

We know there are six classes (the first sentence of the setup). If you count up the different classes on the diagram, you’ll see there are seven groups. That’s too many. 

But there’s no mistake. This just means that two of the groups will be merged: either 0 or H will go with P. Here’s how to draw it:

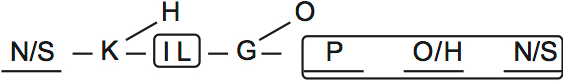
One of O and H goes with P, and so does one of N and S. 

I left the other H and O on the diagram. It’s not a problem to repeat variables, as long as you understand what they mean. Obviously if H is in the class with P, for example, then there’s no separate class with H alone. It would look like this:

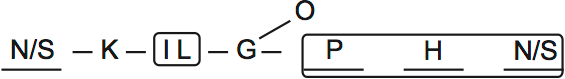
I didn’t draw that separately when I did the game myself, because it seemed more effective in this case to show the different possibilities within the same main diagram. But feel free to draw the separate diagrams.

Another possibility is that both O and H go with P. We still have one of N/S left to place. They can go anywhere. It’s even possible to put both N and S before K.

The circle around N/S means that they are random. One of either N or S can go anywhere.

---