LSAT 32, Game 2 Setup, Works, LSATHacks

This is an explanation of the second logic game from Section III of LSAT Preptest 32, the October 2000 LSAT.

A reading club organizer will select five or six works from a group of nine works. There are six novels (n) in total: three in French (F) and three in Russian (R). There are also two French plays (p), and one Russian play. You must decide which works will be selected depending on the rules.

Game Setup

Numbers are very important for this game. It’s also important to learn all of the rules by heart, or number them in a list. 

Some games depend on mastery of the rules, and this is one of them. There are deductions to be made, but they come from thoroughly understanding the rules.

I want to draw attention to the last two rules, as they can lead to confusion. Rule three says you can’t have more Russian than French novels. Since we have either three or four novels, this means that at least two French novels must be chosen. Otherwise the Russian novels will outnumber the French.

There are only three plays: French, French and Russian. The fourth rule effectively tells us that we can never have all three plays. If we have both French plays, we lose the Russian.

So the maximum number of plays is: two.

Before starting, you should think about how everything works together. For instance, if there are six works, then we must have four novels and two plays, thanks to rule 2 and rule 4. 

Its useful to start with the scenario where there are six works, because it’s more limited. Here it is:

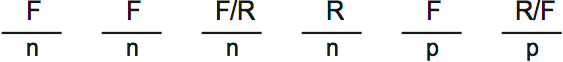
There has to be at least one French play, because there’s only one Russian play. If you have more than one play, one of them will have to be French.

There can be at most three French novels, because there only are three French novels.

There are at least two French novels. If there were only one French novel, then Russian novels would outnumber the French novels. Rule 3 doesn’t allow that.

There are two possibilities if only five works are selected. We could have three novels and two plays:

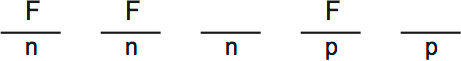
At least two novels are French, to prevent Russian novels from outnumbering French novels (rule 3). One play is French, because there is, at most, only one Russian play to select.

Or we could select four novels and one play:

At least two novels are French, to prevent Russian novels from outnumbering French novels (rule 3). 

One novel is Russian, because there are only three French novels.

The other novels and the play could be French or Russian. The only other restriction is that they can’t all be French (rule 1).

Note that in every case we need at least two French novels, and at least one play.

Rules and deductions to remember:

1. No more than four French works (rule 1)
2. Three or Four novels (rule 2)
3. At least two French novels (rule 3)
4. Max two of three plays (rule 4)

You don’t need the scenarios I drew. But thinking through them helps make this game a lot easier.

In case you wondered how I have time for that – I don’t always do all this work upfront. Sometimes I do it while doing the questions, as the game becomes clearer. But I do do the work, it makes the game clearer and I get the answers faster.

LawHub Order

LawHub Order

---