LSAT 33, Game 3 Setup, Stones, LSATHacks

This is an explanation of the third logic game from Section IV of LSAT Preptest 33, the December 2000 LSAT.

A jeweler has a selection of ten stones. There are three rubies (r: F, G, H); three sapphires (s: J, K, M); and four topazes (t: W, X, Y, Z). The jeweler must choose six of these stones to make six rings.

Game Setup

Numbers are very important in this unusual game. The jeweler will pick six out of ten stones.

Your first step should be listing your variables, since the variable list is unusually important for this game:

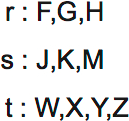
Note that rubies are early in the alphabet, sapphires are in the middle, and topazes are late in the alphabet. LSAT variables often follow this pattern, which makes them easier to remember. 

At least two topazes are selected. This is extremely important to remember, and you should internalize it somehow. There’s no magic symbol that will make this work. You can draw “2” beside topazes, or something equivalent. 

Just find some way to commit it to memory.

The next rule is also important:

Two sapphires lead to one ruby, which leads to three topazes, because we need six gems. You must remember that having two sapphires is special. 

The next two rules can be connected. If M is in, W is in. And if W is in, H and Z are out. I’ve also shown the contrapositive:

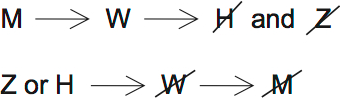
You can’t have both W and Z at the same time. W and Z are both topazes, and you need at least two topazes.

So if you can have at most one of W and Z, then you must need at least one of the other topazes: Y or X.

This deduction solves question 17.

If you want, you can draw this in a table as a reminder:

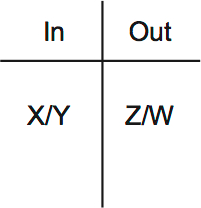
One of X and Y is in, and one of Z and W are out.

There is one more major deduction, that comes in question 14. We need three stones from at least one of the types of stones. There’s no other way to get six. 

We can’t have two of each type, because if we have two sapphires, rule 2 comes into effect.

We can’t have four topazes and two of another type, because W and Z can’t be together. 

If we try one sapphire, and fewer than three rubies and three topazes, then we can’t get six stones.

So we need three of one type. The possible numerical distributions are:

1. 3 and 3
2. 3, 2 and 1

I’ll talk about this more in question 14, which is the question that tests this deduction. This is a hard deduction. Almost no one gets it during the setup, the first time they do the game.

---