This is an explanation of the second logic game from Section IV of LSAT Preptest 34, the June 2001 LSAT.
Five philosophy lectures will be given each week for five consecutive weeks. The five lectures will focus on six philosophers, namely: Kant, Lock, Mille, Nietzsche, Ockham, and Plato (K, L, M, N, O, P).
Game Setup
This is another linear game, but it plays out differently from most linear games. We’re trying to determine the lecture topic for each of five days. The topics can’t repeat. This is the major limiting factor.
There are five lecturers. Each can only lecture about certain philosophers. They lecture in order, one each day for five days. We can draw the speakers horizontally. Underneath we can put the possible lecture topics they can cover.
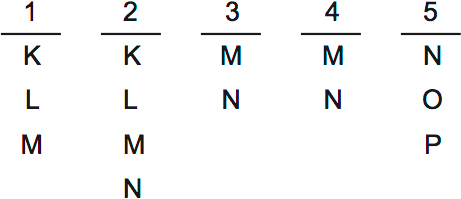
Take a look at 3 and 4. They don’t have many options: only M or N. If 3 lectures about M, then 4 can only speak about N, and vice-versa.
This means that 3 and 4 have to talk about M. No one else can lecture about M and N!
So 1 and 2 can only lecture about K and L. 5 can only lecture about O or P.
It doesn’t matter which of 1 and 2 lectures about K or L. The speakers are quite interchangeable. It’s the same for 3 and 4. The key to the game simply lies in knowing what each speaker’s (limited) options are. This next diagram shows which topics each speaker can lecture about.
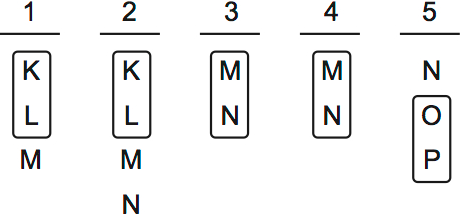
There’s nothing else to do. This diagram will let us answer every question with ease.


Why does Lecturer 4 have to talk about only M or N? There is no condition that states that.
Thanks
Disregard. Misread. Thanks.