LSAT 65, Game 3 Setup, Luncheon, LSATHacks

This is an explanation of the third logic game from Section II of LSAT Preptest 65, the December 2011 LSAT.

A luncheon organizer will serve five foods from a selection of eight. The eight foods are: two desserts (F, G), three main courses (N, O, P) and three side dishes (T, V, W). Three of the eight are hot foods (F, N, T).

Game Setup

This is a grouping game. You need a firm grasp of the rules to solve this game. Make sure you’ve reread them before reading this explanation.

I set this game up using an in-out diagram (drawn later). I usually don’t use this type of diagram, but for this game I found it extremely useful to be able to show which variables are out. 

This is because the game often places three variables out, which means that all the other variables are in.

There are two things I want to point out. First, it’s fine to modify your diagramming style based on circumstances.

Second, you don’t have to do games perfectly. I didn’t use an in-out diagram when I first did this game. I got everything right, but I struggled.

When I sat down to explain it, I realized an in-out diagram would be much simpler. 

So my original diagram wasn’t the same as my final diagram. You might ask: why bother studying these final diagrams then?

Well, even though I didn’t draw an in-out diagram, I was very aware of which variables are out. That comes with practice, and from having drawn ‘out’ diagrams on previous games.

So by practicing with the best diagrams, you’ll stand a better shot of coming up with great diagrams when you see new games. And even if you don’t get the ideal diagram, your intuition will be better for having studied ideal diagrams.

Ok, on to the rules. There are eight foods, and five of them are included. Take note whenever a game includes only some of the variables. We know, for instance, that if three variables are left out, then the other five must be in. This comes up a lot in this game.

The dishes are desserts, main courses, and sides. Some are hot. Here’s the list. I indicated the hot foods by putting a box around them.

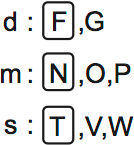
You could draw a separate list of hot foods, but it’s best to stick to the smallest possible number of diagrams. That makes it easier to see the whole setup.

Here’s the in/out diagram I mentioned earlier. I included the first rule directly on it. That rule says that at least one dessert, main course and side dish are in:

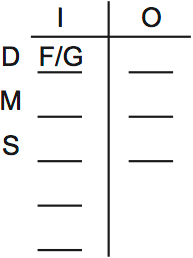
I included one slot for dessert, main course, and side dishes. Note that these only refer to the in group. The out group can be any type of dish. 

There are only two desserts: F and G. So at least one of F and G is in. I drew that on the diagram. 

Rule two I just memorized: it says you always need at least one hot food. You could draw ‘1+ Hot’ in your list of rules if you prefer.

Rule three says either PW are both in, or both out:

Rule four says that if G is in, O is in:

Rule five says that if N is in, V is out:

If you’re still making mistakes or forgetting contrapositives, you should draw the contrapositives for rules four and five. Otherwise it’s not necessary. Here are the contrapositives:

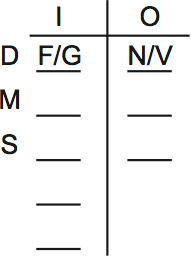
Rule five is important. One of N or V is always out. This type of rule comes up again and again on logic games. 

N and V could both be out together, mind you. The rule doesn’t say ‘if N is out, V is in’. 

But at least one always has to be out. You can put this deduction on the main diagram:

We could stop here. But there’s one more deduction which is somewhat useful.

It has to do with the third rule. PW are either in or out. When the game gives you only two possibilities, you should try both of them. This usually leads to deductions.

Not much happens if we put PW in. Still, this lets us view the scenario more clearly.:

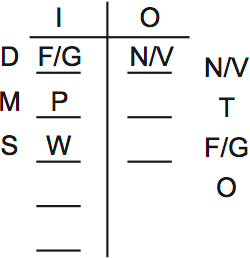
I drew the remaining variables to the right of the diagram. It’s much easier to visualize combinations when the open slots and remaining variables are written down in front of you.

Note that I put P and W in the M and S slots. This makes it clear that rule one is fulfilled in this scenario. 

Now, if we put PW out, then three variables are out: P, W, and one of N/V.

That means everyone else is in!

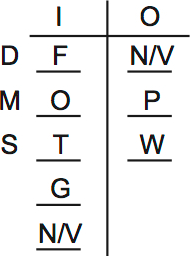
So if PW are out, then the only uncertainty is which of N or V is in.

I actually don’t use these scenarios very much in the explanations. But I’m definitely aware of them, and you should be too. 

Studying these deductions upfront is worthwhile. Sometimes you’ll get them, and even if you don’t your intuition will be better.

---