LSAT 72, Game 2 Setup, Five Houses, LSATHacks

This is an explanation of the second logic game from Section IV of LSAT Preptest 72, the June 2014 LSAT.

A realtor will show five houses to a client in a single day. Each house will be only shown. The houses are from five different neighborhoods: Quarry, Riverton, Shelburne, Townsend, and Valencia (Q, R, S, T, V). You must determine the orders in which the houses can be shown based on the rules.

Game Setup

This game is unusual in that you can draw four scenarios that cover absolutely every possibility. This used to be common on older games, but I don’t see it much on new games.

Typically, I don’t draw more than two scenarios, because the possibilities are too open ended. But in this case, the four scenarios were very, very useful. 

When I made them it was obvious the game was quite restricted, that’s why I drew more than four. When I redid this game I timed myself, and with the scenarios I finished in 3 minutes 30 seconds!

Let’s talk about how to draw the scenarios. You need a good grasp of the rules and how they interact. 

• R is first or second. 
• T is first or fifth

So if R is first, T is fifth. And if T is first, R is second. That’s one major restriction. Next major rule:

• Q or V is third

Again, a major restriction. If one isn’t third, the other is. Final major restriction:

• Q cannot be beside S.

This often determines whether Q or V is third.

Look over those rules to make sure you know them. Now, let’s make some scenarios, using R and T as limiting factors. The first scenario has R first. The second third scenarios have R second and T fifth. The fourth scenario has T first.

Scenario 1: R first, T fifth

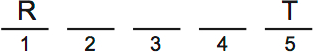
Next, we need to place Q, S and V. Q can’t be third, because then it would be beside S no matter where S went. 

So V is third, and Q/S are split between second and fourth:

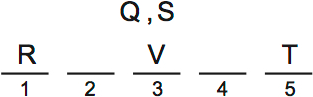
(Q, S comma indicates they fill the remaining slots and are reversible. I often prefer this to drawing Q/S)

Scenario 2: R second, T fifth, Q third

If R is second, there are two possibilities: T first or T fifth. This scenario is T fifth.

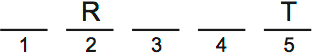
Next, either Q or V can be third. For this scenario, we’ll put Q third

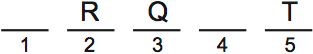
Q and S can’t be together, so this means S is first and V is fourth.

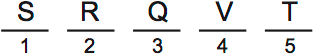
Scenario 3: R second, T fifth, V third

If R is second, there are two possibilities: T first or T fifth. This scenario is T fifth.

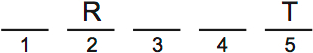
In scenario 2, we placed Q third. In this scenario, we’ll place V third (either Q or V has to go third):

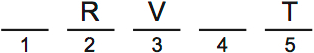
Now Q and S are interchangeable:

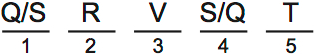
Note: I’ve drawn the interchangeability differently than I did in scenario 1. For some reason, the Q/S method felt more natural here. Choose whichever method you like, they mean the same thing.

Scenario 4: R second, T first

If R is second, there are two possibilities: T first or T fifth. We already drew the two T fifth scenarios. This scenario is T first.

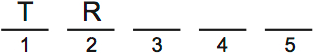
Now we have to place Q, V and S. Q or V has to go third. We can’t put V third, because then QS would be in fourth and fifth, and they can’t go beside each other.

So Q is third, V is fourth and S is fifth:

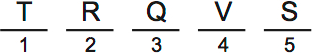
Those are all the scenarios. If any of them don’t make sense, reread the rules, and try drawing them yourself. Probably you’ve missed one of the rules.

The key to logic games is that everything happens for a reason, and the rules are the reason. To truly understand a game you must know the rules like the back of your hand.

Mind you, it’s a good idea to try building the four scenarios yourself anyway, even if you understand them. These scenarios are excellent practice for the kind of sequential deductions that are tested again and again on logic games.

Note: On the questions, I’ll expect you to be aware of the four scenarios. I’ve listed them more close together in the main diagram section. I’ll reference scenarios in the questions by number.

---