LG Game 4 Question 23 Explanation, by LSATHacks
This was a tricky question. I had to solve it by brute force elimination. We’re looking for something that can’t be true. So any answer that’s possible is wrong. To eliminate an answer, you just need to construct a working scenario that shows it’s possible.
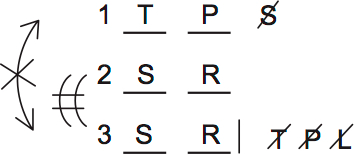
I first checked past questions to see if they proved any answers were possible. The correct answer to question 19 proves that A is possible.
This diagram from question 21 proves that B is possible:
This scenario proves that D is possible:
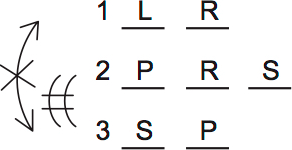
This scenario proves that E is possible:
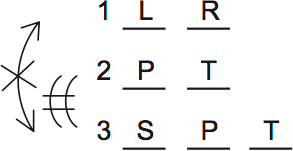
Note: Brute force is slower, but it doesn’t have to be slow. Practice making scenarios quickly. The biggest danger is hesitation. If you know the rules, and draw without hesitating, you can draw a correct scenario in 5-10 seconds.
C is CORRECT. Bouquet 2 can’t have only L, P and R. This is a little tricky to prove. Let’s go step by step. First, place LPR in bouquet 2:
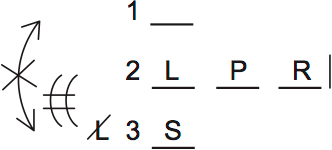
Next, apply rule 2: bouquets 2 and 3 need two flowers in common. Bouquet 3 can’t have lilies, so it must have peonies and roses:
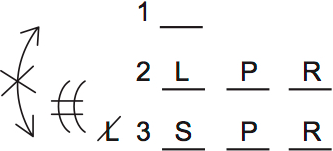
Next, apply rule 1: Bouquets 1 and 3 can’t share flowers. So bouquet 1 can’t have S, P or R:
But, bouquet 1 needs at least one flower. And this is why C doesn’t work. The only flowers left are tulips and lilies. But neither work: tulips require peonies, and lilies require roses.
So C is impossible, and therefore CORRECT.
This question is actually not that difficult to solve. B2 and B3 must have exactly two flowers in common–not at least two. Given that B3 must have snapdragons, B2 can not contain a list of flowers that excludes snapdragons. Choice C doesn’t have any snappers, so it’s gotta be wrong.
but how could you know if the answer choice is only showing one possibility instead of the complete list, which could exclude S
Think about the connection between 1 and 3, and that they can’t share any flowers. Two of the flowers force an addition, that being L= +R, and T= +P.
We can’t add L as the common flower between 2 and 3 because it eliminates S which is a must in 3. But when adding P and R between 2 and 3, what’s left for 1 that isn’t included in 3? L and T, but that creates the problem of adding R and P, thus it doesn’t work.