This is an explanation of the first logic game from Section IV of LSAT Preptest 75, the June 2015 LSAT.
A company’s HR department must determine the bonuses of 7 employees from two different departments. Kimura, Lopez, Meng, and Peterson (K, L, M, P) work in the Finance department while Vaughan, Xavier, and Zane (V, X, Z) work in the Graphics department. Each employee can get a $1,000, $3,000 or $5,000 bonus. You must determine the possible distribution of the bonuses according to the rules.
Game Setup
This game combines linear and grouping elements. On recent LSATs the LSAC has been making more unique, unusual games. I do not believe these games are harder than past games. I merely think they are different.
For new LSATs, you should not focus on memorizing game “types”. The people who are the very best at logic games do not decide how to approach a game based on type. They just focus on what the rules say.
Your best approach is to work through past games to mastery, so that you know how different rules work and what constraints within games will have large effects. This will let you quickly and correctly solve unusual games, like this one.
Also, don’t use explanations too much, including mine. To beat these unusual games you need to practice figuring out games on your own, before checking outside resources. You can learn a lot by repeating games before checking explanations.
This game splits seven employees across two groups: Finance and Graphics. It’s best to represent the two groups like this:
![]()
One key to games is having all of the elements present so you can use them. It’s important that elements be close to each other. If you have to search to find things, you are taking away short-term working memory that could be spent on solving the question.
In this case, I initially made my list of variables directly above each diagram:
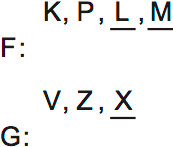
I’ve also underlined L, M and X to cover the final two rules:
- Lopez, Meng and Xavier are highly effective.
- The highly effective people have a higher bonus than the others.
That covers rules two and three. Note that I don’t always draw the rules in order. I want a clear, logical diagram. I don’t know how best to draw things until I’ve read all the rules. I draw them in the order that makes the most sense, once I’ve read them all.
Ok, so now only the first rule is left: no one in Graphics gets a $1,000 bonus. That means graphics employees can only get $3,000 or $5,000 bonuses.
We know that Xavier has a higher bonus than Vaughan and Zane, thanks to rules two and three combined. So that means Xavier has a $5,000 bonus, while the other two only earn $3,000:
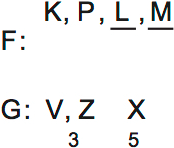
So everything is determined for the graphics department.
The finance department, on the other hand, is more flexible. We know that L and M are higher than K and P. But that’s all we know.
If I’ve counted correctly, there are twenty ways we could arrange the bonuses in the finance department. It’s inefficient to draw them all.
So the graphics department is fully determined, and already on the diagram. You only need to remember two things:
- The bonuses are $1,000, $3,000 and $5,000
- L and M have higher bonuses than K and P
The questions will do the rest. A question will give you something like “Lopez and Meng get different bonuses”. That immediately cuts the possibilities down to one diagram: K and P have $1000, and one of L/M gets $3000 and the other gets $5000. It’s much simpler to wait for the questions to narrow things down before you spend brainpower figuring out possibilities.
On the setup, stick to what must be true.

Want a free Logic Games lesson?
Get a free sample of the Logic Games Mastery Seminar. Learn tips for going faster at logic games


This is one of the first mixed setup games I knocked out of the park, under time, and was fully confident in. Your explanation helped make sure I fully understood it!
How did you count 20 possibilities for the finance group? I found that there were 4 possibilities for L and M: both 5, both 3, 3 and 5 or 5 and 3. In any case where L or M gets 3, K and P must get 1. That accounts for 3 possibilities (5-3-1-1, 3-5-1-1, and 3-3-1-1). If L and M both get 5, then you have a similar situation with K and P: Both 1, both 3, 1/3, or 3/1. That’s another 4 possibilities for a total of 7.