LSAT 78, Game 3 Setup, Antique Auction, LSATHacks

Game Setup

Time on second attempt: 8:10

See “repeating games” at bottom of section

—————

This is a hard game, which is unusual for a sequencing game. After doing it three times, I came to the conclusion that the game is easier to solve by dividing the setup into three clear scenarios. With that, I easily solved all the questions.

But, it took me three tries to do that! So it is worth it for you to learn how to make the scenarios? 

Yes, I think so. Even if you don’t manage to get scenarios like this on all games, I think learning the process of generating them will help you create them on a larger percentage of games.

I’m going to first show the deductions I made during the setup when I first did the game timed. Then I’ll show the scenarios, and use those to solve the questions.

The Rules

This was a sequencing game, which makes it especially interesting that it was difficult. Normally, sequencing games are so easy to practice that none of them are challenging once you’ve mastered the basic form. Clearly, LSAC has put some thought into how to make these more difficult.

On sequencing games, I always start with the easiest rules to diagram. Here, that’s rules 1 and 3. 

Those rules say that S isn’t first, and S is earlier than M and V:

The blank space in front of S is a reminder that S can’t go first. This turned out to be the key to the game, for me.

Of course, you could just draw a “not rule” for S under slot 1, like this:

This is logically correct, but it’s not very helpful. It’s hard to combine with the other rules. Whereas drawing the blank space in front of S helped me make further deductions, and also helped me remember the rule in all contexts.

I approach rules from easiest to hardest. So let’s look at rule 4 next. Rule 2 can only be fully understood once we’ve drawn everything else.

Rule 4 says that T is earlier than one of H or V, but not the other. A lot of people draw this as “T – H or T – V”. Again, this is logically correct, but it’s not effective. Here’s how you should draw it:

Why? Because, if T can’t be before both H and V, but must be before one of them, then that means it must be between them. This is a common rule type on newer sequencing games, so you should learn to recognize the pattern.

Now we can turn to rule 2. This rule says that if H is before L, then M is also before L. Drawn alone, this isn’t that complicated:

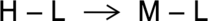
The rules I’ve drawn above are all that I drew when I first tried this game. But, as I wrote above, we can combine the rules into three definite scenarios, starting with rule 2. Let’s see how.

We already have M and V in the other diagram. So, there must be a way to combine these two rules. We can make a version for two scenarios:

• Where H is before L (and the rule applies)
• Where L is not before H (and the rule does not apply)

Let’s try H before L first. We’ll call this scenario 1.

Scenario 1

Here’s the diagram we get. If H is before L, then we must draw both H and M before L. 

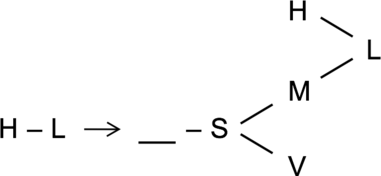
The diagram above already covers rules 1, 2 and 3. There are two open questions:

• How does rule 4 affect it? (H, T, V)
• Who can go first?

On this diagram, someone has to go in front of S, and only T or H are left to go in front of S. (H can go first: the only rule for H on this diagram is that they are before L. First is before L).

But look carefully at rule 4. T is always in the middle of V and H. So T can’t go first. 

So that leaves H. And since H is first, the order for rule 4 is H – T – V

So on the diagram, we can draw T before V and after H:

Note that the only thing that affects position are lines between two variables. So, for example. since there are no lines between V and L, either one of them could go last.

So that’s scenario 1, where H is before L. Now let’s look at what happens if we put L before H.

Scenarios 2 and 3

Here’s the diagram we’re starting from:

We already placed H before L. Now we’re placing L before H. But that doesn’t trigger any rules, so can we really make any deductions? 

Well, we saw that the first position is fairly restricted. Let’s see who can go first if L is before H.

• Not S, M, or V. The diagram shows they aren’t first.
• Not H, since we put it after L.
• Not T, because T is always in the middle of H and V (rule 4)

So if H isn’t first, then L is! So we can put L first, and also draw H after L, like this: 

The T is sort of floating up above to the right. Note that though V is visually after H, V could go before H in this diagram.

Now, are we done? Not quite. The diagram above covers rules 1-3. But we haven’t applied rule 4, the one that says T is between V and H, in either order. 

We can construct two more scenarios by placing them in both orders:

• H – T – V
• V – T – H

Here they are:

Scenario 2

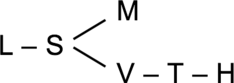
Scenario 3

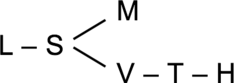
These diagrams are potentially confusing though. To read them, you must remember that there is only a relationship between variables if they are connected by lines. (e.g. S is before M because a line connects them)

But in, for example, scenario 2, S could be either before or after T. There are no lines connecting S and T.

I know sequencing diagrams well enough to avoid getting mixed up by this, but I would be careful drawing this type of diagram until you can avoid the error of thinking that left/right placement matters.

Here are all three scenarios, plus what triggers them.

Scenario 1 ( H before L)

Scenario 2 (L before H, H – T – V)

Scenario 3 (L before H, V – T – H)

You could also solve this game just by drawing the rules and making deductions. But I think you’ll find this method faster. If you prefer to try the rules based approach, here are the rules:

—————

Repeating Games

I’ve written elsewhere about the benefits of repeating games, to solidify your intuition for deductions. Note that the purpose of repeating games is to prove the answers right, so it doesn’t matter if you remember the right answer.

I repeated this game about three days after I first saw it, by which time I had forgotten the answers. I’ve written how long it took me on the second attempt. That time, or a couple minutes above it, is roughly the standard you should be aspiring to – a lot of people take 8-9 minutes on a repeat attempt, get everything right, and pat themselves on the back. But that’s too slow. The faster you go when repeating, the faster you’ll learn to go the first time you see a game.

(I say “a couple minutes above” my time because, after years of teaching the LSAT, I’m really, really fast. You should be almost as fast as me, but you don’t exactly need to match my pace to score -0.)

Time on second attempt: 8:10

Quick Jump PT Section Que