What is a Negation?

Negations are an important concept to master if you’re seriously looking to improve at logical reasoning, but tricky to get the hang of. When you think of a negation, you may be conceptualizing it as an opposite. However, there are important distinctions between the two, and you will find that an opposite is often much stronger than a logical negation. For example, the opposite of “up” is down”, while the negation of “up” is simply “not up”. The negation of “fire” isn’t “water”, it’s “not fire”. The negation of “all” isn’t “none”, it’s “not all”. You want to make sure you aren’t going overboard when negating!

We only want to change enough that the statement is false. This can usually be accomplished by adding a “not” before the word we are negating, but there are some rules to remember. We have to know how to negate different types of statements.

Quantitative Statements

The first type of statement we’ll tackle here is a quantitative statement. These are statements that use words like “all”, “some”, “most”, “none”, or any similar words. We’ll go through these one by one.

“All” Statements

“All” statements are pretty simple. If you say “All of my friends like horror movies”, it’s clear what you mean: every single one of your friends likes horror movies. But how do we negate this?

Remember, as I mentioned above – the negation of “all” isn’t “none”! “None of my friends like horror movies” is way too strong. Instead, let’s add the word “not”: “Not all of my friends like horror movies”. Here, we see that there could still be friends who like horror movies, but there are also definitely some who do not like horror movies – because we know not all of them do. It’s important to note that this could mean that none of your friends like horror movies, but we don’t know for certain.

​”Some” Statements

Next, we’ll look at “some”. If you say “Some of the students in my class failed the test”, we know that there is at least one student in your class who failed. It could be that all of the students failed the test! But all we know is that there is at least one.

You may be tempted to negate this as “Some of the students in my class did not fail the test”, but this is not a negation of the original statement. It could be true that some students failed, and some students did not fail. What you should really be negating is the quantity. “Not some” is a bit clunky to think about, but you just have to remember that the negation of “some” is “none”. So our negation is “None of the students in my class failed the test”.

​”Most” Statements

“Most” statements are pretty straightforward. If you say “Most clowns wear red noses”, it means that more than half of clowns wear red noses. This could be all clowns, but it cannot be half or less of clowns. The negation of “most” is “not most”, and unfortunately there is no common English word that means the same thing. Remember that “not most” includes all possibilities that don’t fall under “most”. Therefore, “not most” could be anywhere from “none” to “half”, but no greater.

The negation of our “most” statement, then, could be “no more than half of all clowns wear red noses”. This is anywhere from 0% to 50% of clowns, whereas “most clowns” would be 51% to 100%. Note that other words, like “usually” or “probably”, follow similar rules on the LSAT.

​”None” Statements

Finally, we have “none” statements. An example of a “none” statement could be “None of the restaurants around me are hiring”. None can only mean one thing: zero. The negation of none, then, is “not none”, which is the same as some. It can be any amount, even the full amount, as long as it’s not zero. The negation of our example statement would be “Some of the restaurants around me are hiring”.

Here is a chart you can keep handy until you’ve got a solid grasp on negating quantitative statements.

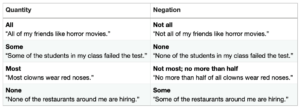
One helpful trick to know if you’ve correctly negated a qualitative statement: a statement and its negation will cover all ranges and never overlap. Look at our “some” statement, for example. Either some students failed the test, or no students failed the test. Some can be any non-zero number of students, whereas none has to be zero. There is no overlap, and between our two statements we’ve covered all the possibilities – there’s no other amount of students that could have failed the test.​

Conditional Statements

Conditional statements can be tricky to negate if you don’t have the hang of them. Here is an example of a conditional statement – try to negate it before you read onward:

“If I eat cake for breakfast, I will feel sick in the afternoon.”

Your first thought might have been to change it to this:

“If I eat cake for breakfast, I won’t feel sick in the afternoon”.

If you did do this, you’ve fallen into the common mistake of negating too strongly. You can actually think of conditional statements like “all” statements, and rewrite them like so:

“On all days where I eat cake for breakfast, I feel sick in the afternoon.”

Based on what we learned about quantitative statements above, the negation is:

“On days where I eat cake for breakfast, I don’t always feel sick in the afternoon”.

Or,

“If I eat cake for breakfast, I might not feel sick in the afternoon”.

As you can see, the negation of “I will” isn’t “I won’t”, it’s “I might not”! This strategy can help you to conceptualize conditional statements more easily, but it would be good to practice until you can do them without needing to convert to qualitative statements and back.

Here’s another example:

“If you got accepted to law school, you had a good LSAT score.”

If you wanted to make it an “all” statement, you could change it to this:

“All people who got accepted to law school had a good LSAT score.”

Then, you can negate it like so:

“Not all people who got accepted to law school had a good LSAT score.”

Or,

“Even if you got into law school, you might not have had a good LSAT score.”

One last thing about conditional statements: if you see “might”, it’s similar to “some”. “Might” means “there’s some chance” – so the negation of a “might” statement is a “won’t” statement. Similarly, the negation of a “might not” statement is a “will” statement.

Compound Statements

There are two main types of compound statements: “and” statements and “or” statements.

“And” Statements

“And” statements require at least two things to be true. To negate them, we have to make at least one of those things false. Here is an example:

“My son and my daughter like cucumbers.”

To negate this, we only need one of the kids to not like cucumbers. If both of the kids dislike cucumbers, that’s okay too – as long as they don’t both like them. The negation can be written in two ways:

“Either my son or my daughter might like cucumbers, but not both of them.”

“Either my son, my daughter, or both of them dislike cucumbers.”

“Or” Statements​

“Or” statements only require one thing to be true. To negate these, we need both to be false.

“Company A will be bought out by Company B or Company C.”

We need both of these to be false. This looks like so:

“Company A will not be bought out by Company B or Company C.”

​

This might seem abstract, but you’ve probably already done it when taking the contrapositive of a conditional statement:

A ➞ B and C
~B or ~C ➞ ~A

The negated sufficient condition is a “not both” statement. So every time you take the contrapositive of a compound statement, you are negating a compound statement.

When are Negations Useful?

The negation test is often used in Necessary Assumption questions to check answers. You can negate all the answer choices, and check them against the argument. If the argument falls apart when the negated answer is assumed, then the original answer is the necessary assumption.

I’ve linked below an example in which I applied the negation test to a LR question (specifically Preptest 81, LRI, Q5).

Negating is sometimes also necessary to parse what an argument is trying to say. Take this example.

“Some reviewers said Scooby-Doo is the funniest dog on television. But those reviewers are wrong.”

The author clearly disagrees with the reviewers, but we don’t know where their actual opinion stands. It would be wrong to say that the author thinks Scooby-Doo is the least funny dog on television. This is too strong. The author’s actual stance, from what we know, is that Scooby-Doo is not the funniest dog on television. This is the negation of the reviewers’ belief. He could still be the second-funniest, or the least funny, or anywhere in between.

Negations can also be used to determine whether an argument is flawed. Consider this argument:

“I made more money this year than my friend Stuart. Therefore, I must have worked more hours than Stuart did.”

Is it possible for the argument’s conclusion to be false? In order to see if the conclusion holds up, we can negate it. If it makes no sense, then the author has properly drawn the conclusion. This statement is negated like so:

“I made more money this year than my friend Stuart. However, I did not work more hours than Stuart did.”

Is this statement possible? You may have already realized that the answer is yes – if the author makes more money per hour than Stuart, then they could have worked the same or fewer hours than Stuart while still making more money. Because the negation of the conclusion is possible, the conclusion was improperly drawn.

As mentioned above, negation techniques are also used when taking contrapositives of conditional statements. This is something you probably commonly do in logic games to infer new rules from what you’re given. Take this statement:

“If I feel rested today, I must have slept for 8 hours and eaten breakfast.”

The contrapositive looks like this:

“If I did not sleep for 8 hours, or I did not eat breakfast, I will not feel rested.”

See how they’re similar?

​How Might Negations Apply to Actual Law?

As with a lot of the logic you use on the LSAT, negations can be useful in interpreting and applying legal principles. The most significant example can be found in criminal law. You’ve heard of “innocent until proven guilty”, right? The government has the burden of proving an accused person committed a crime in order to secure a guilty verdict. A not guilty verdict, on the other hand, can be thought of as the negation of a guilty verdict. The defence doesn’t have to prove that the accused is innocent – rather, they just have to create doubt. The negation of “certainly guilty” is “maybe guilty” – and that’s not enough to secure a guilty verdict.

Further Reading

​LSAT Quantity Words and their Negations [Video]

​How to Go Faster at LSAT Logical Reasoning

​Applying Negation to a Logical Reasoning Question – Example​

​Get the LSAT Course​

​LSAT Course Lesson 6 – covers Necessary Assumption [Video]

​Get the Logical Reasoning Mastery Seminar​

​Logical Reasoning Mastery Seminar Lesson 4 – covers Necessary Assumption [Video]​

​Contrapositives [Video]

Conditional Reasoning on the LSAT

Article Archive