June 2007 LSAT Logic Games Explanations

Time on second attempt: 1:56

See “repeating games” at bottom of section

Note: this game is relatively easy once you’ve mastered LG concepts, so you should aim to be able to finish it extremely quickly. Maybe not in two minutes, but 3-5 is reasonable.

—————

This is a fairly unique game in that it uses numbers, rather than letters, as variables. The only real effects this has are:

• You shouldn’t draw numbers under slots 1-5. This will get confusing.
• You have to do some very minor math: thinking about which numbers are bigger/small, twice as big, etc.

Otherwise, this is a fairly standard linear game. It can be split into two scenarios. The second rule says that the second digit is twice as big as the first. You should look over the numbers and see which numbers could work for that. The only two possibilities are:

1, 2

2, 4

So you can draw this on the diagram. You should also draw the remaining variables which aren’t placed:

The fourth rule says that the third digit is less than the fifth digit. I drew that with an arrow, and a greater-than sign showing that 5th is greater than 3rd:

I also drew two “not” rules. In both diagrams, zero can’t go last, because it is smallest. As for the third slot, you can’t put the biggest number there. So, that means in scenario one it can’t be 3, and in scenario two it can’t be 4.

That’s all there is to this setup! The first two rules just say what the numbers are, and that they appear exactly once.

The Importance of Concise Setups

Notice the features of these diagrams:

• All the rules are on the diagram. You don’t have to think about them.
• All the variables are on the diagram. You don’t have to think about which numbers are left to place in each diagram.

This seems trivial, but it’s not. Logic games are a test of your short term working memory. Humans (that’s you!) can only hold 5-7 facts in their heads at once. We suck at it, basically. And the closer we are to using all of our short term working memory, the worse we work.

Those two bullet points above represent 3-5 items of short term working memory. Placing those 3-5 items on the diagram directly leaves you with basically all of your capacity free. Which is why this game can potentially be done very quickly with a good diagram. (You also need mastery of the forms of logic games, which comes with practice.)

—————

Repeating Games

I’ve written elsewhere about the benefits of repeating games, to solidify your intuition for deductions. Note that the purpose of repeating games is to prove the answers right, so it doesn’t matter if you remember the right answer.

I repeated this game about three days after I first saw it, by which time I had forgotten the answers. I’ve written how long it took me on the second attempt. That time, or a couple minutes above it, is roughly the standard you should be aspiring to – a lot of people take 8-9 minutes on a repeat attempt, get everything right, and pat themselves on the back. But that’s too slow. The faster you go when repeating, the faster you’ll learn to go the first time you see a game.

(I say “a couple minutes above” my time because, after years of teaching the LSAT, I’m really, really fast. You should be almost as fast as me, but you don’t exactly need to match my pace to score -0.)

Time on second attempt: 1:55

The setup section explains how to build this diagram.

Main Diagram

This question says the last digit of the product code is 1. In the setup, we have two scenarios:

In the first scenario, the first digit is 1. So, to place “1” last, we must be in scenario two instead. In that scenario, we can see that the first two digits are “24”.

A is CORRECT. The first digit must be 2.

On general must be true questions, you should look at your diagram to see common features in all scenarios.

Here, the two things we can conclude are:

• 2 is early on
• 0 can’t be last

C is CORRECT. 2 is always before 3, since 2 is either first or second.

This process is called “prephrasing”. You predict what the answer will be, then you skim through the answers looking for that answer.

You should look at all the answers, but when you find your prediction you don’t have to consider every other answer in depth.

This question gives you a new rule. Whenever a question gives you a new rule, you should draw it, and see how it affects the existing rules.

Here, 0 can’t go 3rd, and can’t go 5th. That means 0 must go 4th. C is CORRECT.

There are a few of things to point out.

Focus on restrictions

• Once a variable gets many restrictions, you should consider where it can go. That’s how you get to the “0 must be 4th” deduction.
• You should focus on 0, since it already has restrictions, and this question adds a new one.

Don’t draw, or draw a limited diagram

• You don’t necessarily need to redraw the diagram. At an advanced level, you can just look at your setup and see “oh, this means 0 can’t go 1st, 2nd, 3rd and 5th”
• But, you also don’t need to redraw a full main diagram. This is the diagram I actually drew on my own paper. It’s much faster and conveys the same information:

This question asks about which numbers can’t go third and fourth. You should look at your diagrams for ideas:

The only numbers restricted from going 3rd are 4 and 3, in scenarios 1 and 2, respectively. So you should only look at the answers that place 4 or 3 in 3rd. That’s D and E. So right away you eliminate three answers.

Next, make a diagram showing how 3 could go 3rd (in scenario 1). This will let us see which of the two answers is possible, and therefore wrong.

If we place 3 3rd, then we need 4 5th, in order to obey rule 4 (5th is bigger than 3rd). Therefore, D is possible.

E is CORRECT. We end up with this order: 12340. But, the last digit is supposed to be bigger than the third.

Another general must be true question. We already came up with one general deduction in question 2 (“2 must be early on”). So, that deduction doesn’t work here. Instead, it’s worthwhile to skim the answers and see what the answers look like generally.

You are not trying to solve the question on this step. Just look through to get a sense of them, then return to the main diagram. From doing that, you can see these answers are all about distance between letters.

Next, look to your main diagram and see which variables have fixed positions:

1, 2 and 4 have somewhat fixed positions in at least one of the diagrams. So you should look at answers which use two of those variables. That’s B and E.

B obviously doesn’t have to be true. In the second scenario, 2 is 1st, and 1 isn’t beside 2, so they won’t be exactly one digit apart.

That leaves E. Let’s try drawing 2 and 4 as far apart as we can. In scenario 2, they are beside each other, so we’ll have to use scenario 1. We get this:

E is CORRECT. As you can see, the gap is at most two spaces.

You should read the other answers, but you don’t need to put effort into solving them, since E is consistent with the prephrase. When you review the game afterwards, it is helpful to solve the other answers, but in timed conditions you only need to glance at them to make sure they don’t seem obviously right.

A is wrong for the same reason as B: in scenario one, we see that 1 is first, and 0 isn’t beside 1. So this answer doesn’t need to be true.

Both C and D can be disproved by placing 3 last. This is allowed in both scenarios, and it means 3 is three spaces away from 1 or 2. And we can easily obey rule four by putting 0 third in both cases.

Time on second attempt: 4:38

See “repeating games” at bottom of section

—————

This is a mixed linear/grouping game. It’s also fairly unique. I don’t think I’ve come across a game exactly like this one.

All three rules limit who can go last. So, you should draw those:

Diagram Style

This diagram may be confusing, as I have horizontal lines in two places.

1. The first line is the column, for thursday, friday, saturday
2. The second line indicates the end of the column. E.g. H is last on thursday.

I’ve also drawn smaller letters at the top to show who else can go on that day.

Feel free to draw this diagram another way. What I want you to understand is why each element is there. But there’s nothing wrong with rearranging it and finding your own style.

Why the details make you efficient

The details I listed above might seem trivial, but I’ve found they really help. You can glance at the diagram and instantly see that G and L can go Thursday. You don’t have to think about it while doing the questions, and this makes all the difference on logic games.

That’s all there is to this setup! Except you should note that each movie has to be shown at least once.

It’s also important to note that this game is very flexible. For instance, this is a valid scenario:

It obeys rules 1, 2 and 3. You don’t have to place any other films. You merely have the option to show other films.

—————

Repeating Games

I’ve written elsewhere about the benefits of repeating games, to solidify your intuition for deductions. Note that the purpose of repeating games is to prove the answers right, so it doesn’t matter if you remember the right answer.

I repeated this game about three days after I first saw it, by which time I had forgotten the answers. I’ve written how long it took me on the second attempt. That time, or a couple minutes above it, is roughly the standard you should be aspiring to – a lot of people take 8-9 minutes on a repeat attempt, get everything right, and pat themselves on the back. But that’s too slow. The faster you go when repeating, the faster you’ll learn to go the first time you see a game.

(I say “a couple minutes above” my time because, after years of teaching the LSAT, I’m really, really fast. You should be almost as fast as me, but you don’t exactly need to match my pace to score -0.)

Time on second attempt: 4:38

The setup section explains how to build this diagram.

Main Diagram

For acceptable order questions, go through the rules and use them to eliminate answers one by one.

Note that I use the rules themselves. I don’t use my diagrams for these questions. Reading the rules again for this question will help you memorize them, and it’s also more efficient.

Rule 1 eliminates D. H must go last on Thursday.

Rule 2 eliminates B and E. G or L needs to be last onFriday. And only one of them can go (this is why B is wrong.)

Rule 3 eliminates nothing.

The setup rule eliminates A. Each film has to go at least once, but here, G isn’t shown.

C is CORRECT. It violates no rules.

On general must be false questions, you often can’t make any deductions. Instead, just refer to the diagram when going through the answers:

A is CORRECT. H can’t be shown last on Friday: G or L must be shown last that day. (Rule 2)

In reading the diagram above, it’s vital to know that all of the small letters can go on a day. So, for example, Thursday could be GLH. Or just H, as you choose.

• B: The diagram clearly shows L can go Thursday and Saturday. And we can put L last on Friday.
• C: Put GLH on Thursday. Then on the other two days put G last, and place the other variable that can go on those days in front of G.
• D: All the small letters can go. So just put a different one first each day. G on Thursday, then H and L on Friday and Saturday.
• E: H, G and L are all represented in the films going last. Just put H first, then L, the G, like this:

You don’t even need to place any other films!

This question wants us to place the maximum number of films. But once Greed is shown, we can’t place Limelight. Here’s the main setup diagram for reference:

We need to first figure out who to place last on each day. We should place G last on the final day, in order to maximize the number of times we can place L:

H has to go last on the first day. And since we’re not placing G, we must place L last on the second day.

Next, we want to put as many H’s and L’s as we can. The little letters under each day indicate who is left that can be placed there. We can see those that we can place L thursday, H friday and L saturday:

That’s a total of 6. D is CORRECT.

You might wonder if there’s another way. What if we tried to maximize G instead? We’d get the same result. Above, we drew two H’s, three L’s, and one G. If we instead placed as many G’s as we could, we’d have three G’s, and one L. So it works out the same way. (We’d still have two H’s, because G blocks H on Saturday). Here’s what it looks like:

You don’t need to draw that diagram in timed conditions, as long as you can think through the logic. And it makes sense that putting G last is likely to get the max value, since it lets us fit in three L’s. Basically we have a tradeoff between putting 3G/1L or 3L/1G.

This question places G three times. You should draw that first, since it is the most restricted element: G has to go last on Friday and Saturday.

Note that I’ve put H last on Thursday, because that has to happen. (rule 1)

Now we have to show Harvest once more, and Limelight exactly once. Harvest can only go Friday since G is on Saturday (rule 3):

L can go either Thursday or Saturday, but only once.

E is CORRECT. H and G both must be shown Thursday.

I almost chose B. I had incorrectly drawn L on Saturday only. This is why reading all the answers is important! Once I saw that both B and E were true, I knew I had made a mistake. Don’t just stop when you’ve found the “correct” answer. Glancing at everything is an important check against “stupid” mistakes.

Here’s the main diagram for reference:

This question places L three times. So, you should draw that. That means L will go last on Friday:

L also goes Thursday and Saturday. H must go last on Thursday (rule 1).

This question also says that H goes twice, and G goes once. That means we need one more H, and one G. So, one of them will go last on Saturday. The other will go on Thursday/Friday. (Thursday if it’s G, Friday if it’s H).

This question is asking who could go first on Thursday. It’s either G or L. So, D is CORRECT.

Time on second attempt: 6:42

See “repeating games” at bottom of section

—————

This is a linear game. These are normally easy, but this one has an unusual number of moving parts. I think this is the hardest game on this section.

You should start with the simple rules: T is last, and J can’t be fourth:

When you have one not rule on the diagram, you should look for others. We can add two more, based on the other rules:

• J can’t go first, because it needs G in front (rule 4)
• T can’t go sixth, because variables can’t repeat (rule 5)

Next, draw the other rules. There are two M’s, with at least one G in the middle. J needs G in front of it. And the same variable can’t go together consecutively:

There are two potential traps to avoid on this game:

• J requires G, but G doesn’t require J. So you can have G all on its own.
• GJ can go between the two M’s, fulfilling rules 3 and 4 at once. But this doesn’t have to happen. You can just have G on its own between the M’s.

I don’t think there’s anything else that can be deduced in the setup. The game depends on your skill in applying the rules to specific situations.

—————

Repeating Games

I’ve written elsewhere about the benefits of repeating games, to solidify your intuition for deductions. Note that the purpose of repeating games is to prove the answers right, so it doesn’t matter if you remember the right answer.

I repeated this game about three days after I first saw it, by which time I had forgotten the answers. I’ve written how long it took me on the second attempt. That time, or a couple minutes above it, is roughly the standard you should be aspiring to – a lot of people take 8-9 minutes on a repeat attempt, get everything right, and pat themselves on the back. But that’s too slow. The faster you go when repeating, the faster you’ll learn to go the first time you see a game.

(I say “a couple minutes above” my time because, after years of teaching the LSAT, I’m really, really fast. You should be almost as fast as me, but you don’t exactly need to match my pace to score -0.)

Time on second attempt: 6:42

The setup section explains how to build this diagram.

Main Diagram

For acceptable order questions, go through the rules and use them to eliminate answers one by one.

Note that I use the rules themselves. I don’t use my diagrams for these questions. Reading the rules again for this question will help you memorize them, and it’s also more efficient.

Rule 1 eliminates D. J can’t be fourth.

Rule 2 eliminates E. T must be last.

Rule 3 eliminates B. We need G to be between the two M’s.

Rule 4 eliminates C. We need a G before J (the first one).

A is CORRECT. It violates no rules.

For a general must be true question, you should look at the main diagram to see if there were any deductions beyond what the rules explicitly stated:

Here, there were two:

• T can’t be sixth (rule 5)
• J can’t be first (rule 4)

The first one is A, which is CORRECT.

You should read all the answers to make sure none of the others seem obviously right, of course. This is a good technique to avoid “stupid” mistakes.

This question gives you a new rule. Whenever a question gives you a new rule, you should draw it, and see how it affects the existing rules. Here, the question places T 5th:

You can draw two new not rules. J can’t go sixth; there’s no space for G (rule 4). And T can’t go fourth (rule 5). Right away, this eliminates answer E.

Since we added restrictions, consider who can go fourth and sixth. There are only four destinations. So, if two are out, then only two are left: G or M.

When something can only be two ways, you should split the game into two scenarios and draw both. Here, you could split the game on 4th, or 6th. Either way works. Let’s try sixth. We can make dual scenarios: one with G 6th, and one with M 6th.

Once we have that, the rest of the setup becomes quite restricted, as you’ll see. Let’s put G 6th first.

We still need to place the two M’s, and GJ. Since G has to be between the two M’s, these four variables just fill the first four slots:

Next, let’s place M 6th instead:

This diagram takes a bit more consideration. Remember that only G and M could go 4th and 6th? But now M can’t go 4th either: G must be between the two M’s. And if M were 4th and 6th, there’d be no G in between. So, G is 4th:

Now only M and GJ are left to place. They can go in any order: we have a G between the two M’s no matter which way we do it.

We’ve filled out both scenario (G 6th, M 6th), so now we can find the answer. This question is asking what can be true, so you can just scan through the answers to see which one matches one of the diagrams.

D is CORRECT. It’s the only answer possible in one of the diagrams. (The diagram with G 6th)

Note that these diagrams take many steps to explain, but they needn’t take long to draw. Once you have done many games + repeated sections in order to master games, you can quickly make the deductions I described and draw at the two scenarios.

Practice this until it’s rapid. It should take 20-25 seconds or less, and then the question is basically answered.

This question gives you two new rules. Whenever a question gives you a new rule, you should draw it, and see how it affects the existing rules.

The new rules are that: G is 1st and J is 5th:

J requires G before it (rule 4). So, we can also place G 4th.

Finally, I added some not rules. Rule 5 says destinations can’t be consecutive. So, G can’t go 2nd or 3rd, and J can’t go 6th.

Next, consider that you need two M’s, with a G in between. That takes up at least three spaces. That means M and M can’t go in spaces 2 and 3. So one M must go later, in 6th:

E is CORRECT.

Answers A through C could be true but don’t have to be. D must be false (since M is 6th).

This question gives you two new rules. Whenever a question gives you a new rule, you should draw it, and see how it affects the existing rules.

The new rules are: G is 1st and T is 2nd:

There are four open places. Next, ask yourself who we still have to place. There’s the two M’s, and GJ. That takes up all four slots, and we get this order:

A is CORRECT. The other answers contradict the diagram.

This question gives you a new rule. Whenever a question gives you a new rule, you should draw it, and see how it affects the existing rules.

However, we can’t really deduce anything. And, this question looks suspiciously like question 11: it’s asking us to find an acceptable order.

For acceptable order questions, you should go through the rules and use them to eliminate answers. In this case, the answers all show who is in 4th and 5th. So, just imagine them being in the diagram above, beside M.

Rule 1 eliminates B. J can’t go fourth.

Rule 2 eliminates no rules (we can’t see 7th in the answers)

Rule 3 eliminates E. We end up with MTM in 3-4-5. Whereas we need a G between the M’s.

Rule 4 eliminates D. We need GJ, not TJ.

Rule 5 eliminates C. We can’t have MM. (M is in weeks 3 and 4).

A is CORRECT, by process of elimination. This diagram shows that it works:

This is a general must be true question, and it has the potential to seriously bog you down. Trying every answer would take far too long.

Instead, you should ask who is the most restricted variable. I would say it is J, as it has two rules:

• J can’t go fourth
• J must always have G before it

D has J, and says J makes at most two voyages. If that weren’t true, how many voyages would J make? Three. And that would require three G’s. You’d end up with this:

That doesn’t work. We have a J fourth, and also there’s no space for the two M’s.

D is CORRECT.

For thoroughness, I’ve made some diagrams to disprove the other answers. I didn’t do this in timed conditions, because I was sure D had to be true, and I knew why. I’m including these in case you thought any of the other answers also had to be true.

Of course, on review it is good practice to draw these sorts of diagrams yourself. The more diagrams you practice drawing, the faster you’ll get at it.

This diagram shows that A and E don’t have to be true. G isn’t 1st or 2nd, and the cruise visits T three times:

This diagram shows B doesn’t have to be true:

This diagram shows C doesn’t have to be true. In it, the cruise visits G three times:

Time on second attempt: 6:30

See “repeating games” at bottom of section

—————

This is a grouping game. It’s also comparatively difficult, about as difficult as game 3. There are three groups, which you should draw vertically:

I added a few rules to this diagram. The setup says the centers have at least two, but no more than three materials. So I drew two slots. Then, on the right there is a blank space a vertical line: this shows that each group has space for one more item – but only one more.

These vertical lines are a thing you can use on this type of game to show when a group is closed off. For example, if a group had max two items, you’d draw the vertical line directly to the right of the spaces.

The arrow represents rule 2. Anything in center 2 is also recycled by center 1. Note that there are two possibilities here:

• Center 2 has three materials: center 1 has exactly the same materials.
• Center 2 has two materials: center 1 has those two, but might have a third as well.

Next, you should draw the other rules. W leads to N, and P can only appear once and not with glass:

The second item means that plastic can only appear once, and it can’t go with glass. There are a couple of other ways you could draw this rule. For example:

(You’d also need to list “P = 1”)

Choose whichever version is most intuitive for you. I like the one I chose even though it’s normally a diagram used for linear games (indicating that PG can’t go beside each other, in either order). In my experience I’ve found there’s never been an issue with using this diagram style for both purposes; it feels easiest to me.

I circled both T and N. This is normally done for variables with no rules. So you might wonder why I circled N, since N is related to W.

The reason is that while W places N, N doesn’t actually have any restrictions. So N is very easy to place. Even easier than T, in fact! If you place N, you can place either W or N. Whereas if you place T, you can’t place W.

This “N is easy to place” deduction comes up in many places, and makes the game much simpler.

The other thing to notice is that P and G are hard to place. There are actually only two options for P: it can go in center 1, or center 3. It can’t go in center 2, because anything in 2 also goes in 1. (Meaning P would go twice: in both 1 and 2. But P can only go once.)

Since P can only go in center 1 or 3, we can create two diagrams: One with P in center 1, and one with P in center 3. Let’s draw P in center 1 first:

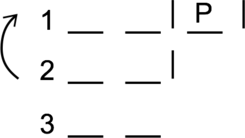
Now, we know P and G can’t go together. That makes G hard to place – where can we put them?

It turns out that if P is in center 1, then G must be in center 3. Why not 2? Because anything in 2 is in 1, and then we would have P and G together.

Now, why have I drawn P in the third position in center 1? Because there is only one P. Which means P isn’t in center 2, but center 1 shares both of the two things from center 2. Which means there must be two open slots in center 1, and only two materials in center 2.

As for the second scenario, it’s simpler: P is in center 3, and G is somewhere in center 1. Centers 1 and 2 could either have 2 or 3 materials.

G can’t be in 3, because G and P can’t go together. So, G must be in either 1 or 2. But, there’s a twist: anything in 2 must be in 1. So, either way, G is in 1!

Another notable deduction: if we are in a scenario with three materials in center 2, it must be in the second scenario.

There’s actually a bit more we can deduce about the first scenario. Who else can go in the two spots shared between centers 1 and 2? Not P, and not G: those are already covered. So the only ones left are W, N and T.

If we place W, we have N. If we place T, who can we place? Not W (that would require N as well), so we have to place N. So whether you place T or W, N is always there:

The second slot in center 3 is relatively open. Anyone except P can go there. Just remember all materials need to be recycled somewhere. So, if T is recycled in 1 and 2, then W (and N) will have to be recycled in center 3.

You don’t need to get these scenarios in advance, of course. But they help. I should note that in my case I actually hadn’t figured out the scenarios explicitly. But, I knew the following two things:

• N seemed easy to place and often had to be placed
• P and G were restricted, and seemed to split between 1 and 3.

—————

Repeating Games

I’ve written elsewhere about the benefits of repeating games, to solidify your intuition for deductions. Note that the purpose of repeating games is to prove the answers right, so it doesn’t matter if you remember the right answer.

I repeated this game about three days after I first saw it, by which time I had forgotten the answers. I’ve written how long it took me on the second attempt. That time, or a couple minutes above it, is roughly the standard you should be aspiring to – a lot of people take 8-9 minutes on a repeat attempt, get everything right, and pat themselves on the back. But that’s too slow. The faster you go when repeating, the faster you’ll learn to go the first time you see a game.

(I say “a couple minutes above” my time because, after years of teaching the LSAT, I’m really, really fast. You should be almost as fast as me, but you don’t exactly need to match my pace to score -0.)

Time on second attempt: 6:30

The setup section explains how to build this diagram.

Main Diagram

Scenario 1

Center 3 will need whatever doesn’t go in 1 and 2. So, if W goes in 1/2, then T must go in 3. If T goes in 1/2, then WN will have to go in 3.

Scenario 2

Rules

For acceptable order questions, go through the rules and use them to eliminate answers one by one.

Note that I use the rules themselves. I don’t use my diagrams for these questions. Reading the rules again for this question will help you memorize them, and it’s also more efficient.

Rule 1 eliminates A. W needs N, in center 3.

Rule 2 eliminates C. All the materials in center 2 need to also be in center 1.

Rule 3 eliminates D and E. In D, you can’t have glass and plastic together. In E, you can’t have plastic in more than one center.

B is CORRECT. It violates no rules.

This question asks where plastic can be recycled. There are three ways to solve this:

1. The setup. If you did the setup scenarios, you already know P can only go in centers 1 and 3.
2. Brute force. Just diagram scenarios proving where P can go.
3. The lazy approach. Use other questions to make scenarios.

Obviously, the setup approach is most efficient. Solving the question in advance is nice, when it happens.

The Lazy Approach

But what do you do if you haven’t? I recommend option 3. Often, drawing scenarios for other questions will help you prove where P can go.

• Question 18 proves that P can go 3rd. The right answer to that question (B) has P in 3rd.
• Question 22 proves that P can go 1st. That question makes you draw this diagram:

So that would make the answer either B or D. The only remaining question is can P go in center 2.

For this, you’d either notice that no other questions had placed P in 2. But, the best way to know that it can’t is logic. P can only go once, but anything placed in center 2 goes twice: in center 2, but also in center 1 (rule 3).

Therefore, D is CORRECT.

This question says center 2 recycles three kinds of material. When that happens, that means center 1 recycles the same three kinds of material (rule 2).

That means that plastic is in center 3, because plastic can only go once. And therefore glass is in centers 1 and 2 (rule 3: PG can’t go together):

That’s enough to solve this question. C is CORRECT.

When you make any deduction on a must be true question, you should always check to see whether it solves the question! There’s no sense doing extra work.

This question is similar to question 20. Question 20 said center 3 had three kinds of material. Here, all centers have three kinds.

The same deduction applies: if centers 2 and 1 have three materials, that means they recycle exactly the same things. Which means center 3 recycles plastic (since plastic can only go once):

G is in centers 1 and 2 because G can’t go with P (rule 3).

This is almost the same as the diagram from question 20, the only difference is that center 3 has three spaces in this diagram.

Since this is a could be true question, you should look for further deductions to narrow down the game. Specifically, who is left to fill the other spaces?

Only T, W and N. How can they be combined? Well, W needs N, so if you place W, it must be as WN. If you don’t place W, you have TN. So, either TN, or WN. In both cases, N is in each center!

I’ve drawn N to the right so it’s visually easier to imagine WN (rule 1). T and W are the only materials left to place: one goes in groups 1 and 2, the other in group 3.

Based on this, D is CORRECT. Center 3 could recycle T, and centers 1 and 2 could recycle W.

In the setup, we saw that G and P are exclusive. So, if G is in center 3, then P must be in center 1:

This is because of the following:

• P and G can’t go together
• Everything in center 2 also goes in center 1; therefore those materials go twice. Since P can only go once, this means it can’t go in center 2.

P is in a 3rd slot in center 1, while center 2 only has two slots. This is because everything in center 2 goes in center 1 as well. So only two things can be shared, since center 1 also needs P.

This question is asking about center 2. What else is left to go in center 2? Only T, W and N. How can they be combined? Either TN, or WN. Why? Because rule 1 says W needs N, so we can’t have WT.

So in either case, N is in groups 1 and 2:

B is CORRECT. Center 2 must recycle newsprint.

The diagram above is actually exactly scenario 1 from the setup. So, if you had found those scenarios in advance, you could solve this question more or less instantly.

This question gives you a new rule. Whenever a question gives you a new rule, you should draw it, and see how it affects the existing rules.

In this case, only center 1 recycles W. Since center 1 has everything that center 2 recycles, that means center 2 only recycles two materials. That’s the only way to leave center 1 the space to recycle W as well:

We know W needs N (rule 1). So we can draw that in both centers 1 and 2. It’s in center 2 because centers 1 and 2 share their first two spaces:

We can make further deductions. P can only be in one center, so it must be in center 3. And glass can’t be in that center, so that means glass must be in centers 1 and 2:

Finally, T has to go somewhere, so they’ll fill a spot in center 3:

Center 3 isn’t closed: N could also go there. But, it doesn’t have to.

This question is asking for the possible combos. They’re:

• GNW
• GN
• PT
• PTN

(The last two are the three different possibilities for center 3)

So, A is CORRECT.