This is an explanation of the fourth logic game from Section II of LSAT Preptest 64, the October 2011 LSAT.
Eight books (F, G, H, I, K, L, M, O) are placed on a three-shelf bookcase. On each of the three shelves – the top shelf (1), the middle shelf (2), and the bottom shelf (3) – there are at least two books. You must determine the placement of the books based on the rules.
Game Setup
This is a grouping game, with a bit of numerical uncertainty. There are at least two books on each shelf, but there are two different possibilities for the number of books on shelves 1 and 2.
That comes from the first rule. The third shelf (bottom) has more books than the first shelf (top). There are eight books in total. Each shelf has to have at least two books. The only way we can put more on the bottom is to put at least three books there and put only two books on the top shelf. These are the two orders, from top to bottom:
2 – 3 – 3
2 – 2 – 4
Both total to 8. If we put three books on the top shelf and four books on the bottom, we’d only have one book left for the middle shelf.
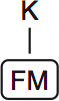
You can draw the last three rules together. K is higher than F and M (which are on the same shelf). O is higher than L. The vertical lines indicate that one variable comes higher than the other.
![]()
It’s best to draw rules 3 and 5 rules together: K is higher than both F and M. I often see students draw rules separately, then get lost on their own page. Drawing a smaller number of rules, together, helps you go faster and avoid mistakes.
We can add those rules to a main diagram. I’ve drawn three horizontal rows to show books on the three bookshelves.
O and K can’t go on the bottom shelf (labelled shelf 3) and L, F and M can’t go on the top shelf. If K were on the bottom, for example, there’d be no way for FM to be below K.
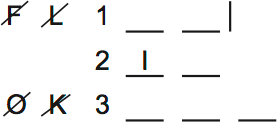
I is on the middle shelf. It’s best to draw that directly on the diagram. Order doesn’t matter, so I just put I on the left.
The vertical line by shelf 1 means that there can only be two books on that shelf.
The lack of a vertical line by the other two shelves means an extra book can be added to one of them. Shelf three has at least three books, because the bottom shelf needs more books than the top shelf.
G and H are random variables, with no rules attached to them (I draw circles around random variables).
![]()
If it helps you visualize things, you could draw two separate shelf setups to show the different numbers of books that could go on the bottom two shelves. One diagram would have four books on the bottom, and one would have three books on the bottom and three on the middle.
I didn’t find that useful. Instead, I thought it was helpful to visualize what happens when F and M go on the second shelf.
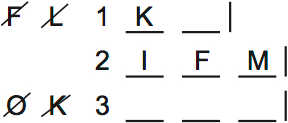
K has to go on the top shelf, because K must go above F.
O has to go on the top shelf too, because O has to go above L.
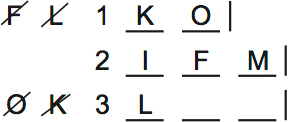
In this case, the random variables G and H are forced to go on the bottom shelf. There’s no space elsewhere.
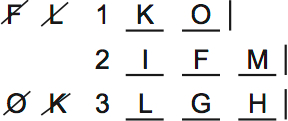
So if F and M are on shelf 2, everything falls into place.
The other scenario (F and M are on the bottom) is less interesting, but it’s still worth drawing. Drawing it will remind you that FM are on the bottom shelf in all scenarios that don’t look like the one I drew above.
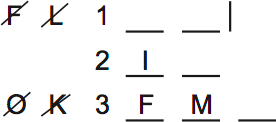

Want a free Logic Games lesson?
Get a free sample of the Logic Games Mastery Seminar. Learn tips for going faster at logic games


Hi John,
You’re right – M cannot be on the top shelf. The reason there isn’t a rule specifying that M is excluded from the top is that in both scenarios diagrammed, M is either on the middle or bottom shelf. It’s not really necessary to include it as a ‘not rule’ on the top shelf, and diagrams should be as simple as possible.
That said, you should diagram games in a way that makes the most sense to you. If putting “not M” on the top shelf makes the game clearer, there’s no reason not to note it.
Thanks for the comment!
Why isn’t M excluded from the top shelf as well? M and F are on the same shelf and F cannot be of the top shelf due to the fact that it is under K, so M should be excluded too, shouldn’t it?