LG Game 4 Question 22 Explanation, by LSATHacks
Having an I in each group restricts things quite heavily.
First, there are no H in this scenario. H’s and I’s can’t go together (rule 4). This eliminates B.
Second, there can be at most 2R in any group in this scenario. I’s and 3R can’t go together (rule 4). This eliminates E.
Third, this means that the only possible variables left to place are 3R, split between groups two and three. There are a total of six variables in this question, at most.
(Note that we don’t need to place any R: it’s possible to place no variables in this game.)
Here’s our base scenario:
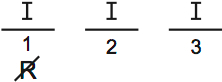
A is CORRECT. Here’s how it looks:
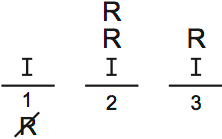
C is wrong because R can’t go in group one. So there’s no way to put anything there apart from the single I we already have.
D is wrong because there are only 3R left to place in those two groups. We have a max of five variables to put in groups 2 and 3.
Hi, I'm Graeme Blake
Founder of LSAThacks; I scored a 177 on the LSAT.
I created the LSAT Mastery Seminars, which are part of the Ultimate LSAT Prep Bundle
If you like the explanations you're reading I'm 100% confident you'll enjoy the courses. Satisfaction guaranteed.
---------
Updates:
For updates, sign up for my email list. I update whenever I have new posts.
Hi,
I was just wondering why there would have to be “3R’s” in this answer.. I understand max of three but couldn’t there be 2R or even 1R
I think I am missing something.
Thanks for your help!
Thanks. I meant we could place 3R at most. I added this line for clarity. We could even place zero R:
(Note that we don’t need to place any R: it’s possible to place no variables in this game.)
Hi,
I’m really not clear on why we only have 3R to split. If I understand correctly, groups 2 and 3 can have at most 2R each, so doesn’t that leave us with 4R to split between the two?
Hi,
Could you please explain the reasoning behind this statement:
“Third, this means that the only possible variables left to place are 3R, split between groups two and three. There are a total of six variables in this question, at most.”
Why can’t there be 4R?