LG Game 4 Setup
This is an explanation of the fourth logic game from Section III of LSAT 70, the October 2013 LSAT.
A naturalist is giving five lectures on different types of birds: osytercatchers, petrels, rails, sandpipers and tern (O, P, R, S, T). The lectures are either in Gladwyn Hall or Howard Auditorium (G, H). You must decide the order of the lectures and which auditorium they take place in.
This is a linear game, with each lecture assigned to one hall.
It’s best to keep your diagrams as simple as possible, so I draw the lectures above the slots, and the halls underneath the slots. I’ll demonstrate by drawing the main diagram with the first and second rules:
Notice that I haven’t included numbers. If you make diagrams without numbers, you’ll very quickly learn to see which slot is which. You’ll also be able to draw diagrams much faster, with less space.
I usually include numbers in my diagrams for explanatory purposes, but with only five slots it’s better to show you how I would actually draw this.
There’s not much we can do with the third rule. It says that three of the lectures are in Gladwyn hall. It’s best just to memorize rules like this, though it’s not a bad idea to include a note in your list of rules, like so:
The most important thing you must realize about the first rule is that if there are three Gs, then there are only two Hs.
This comes up over and over, so I’ll repeat it: there are only two Hs.
The next two rules also can’t be drawn on the diagram. The fourth rule says that S is in Howard Auditorium, and that S is before O:
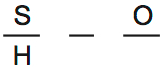
Once again, this diagram includes as much detail as necessary, but no more.
The fifth rule is similar. T is before P, and P takes place in Gladwyn Hall:
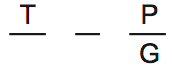
That’s it. As with most modern logic games, there’s no way to combine these rules to draw deductions. The most important things on modern logic games are making a clear representation of the rules, and memorizing the rules.
Is it possible to make a couple of scenarios. We know that there are only two Hs, and S has to take place in H.
S is also in front of O. So either S can go fourth, or S can go in one of 2/3.
If S is fourth, we know that O is last:
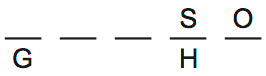
If S is 2/3, then the placement of G and H is completely determined, because we’ve placed both Hs:
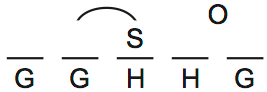
O is floating to the right of S in the second diagram. This is a way of placing the fourth rule directly on the diagram: O is after S. That way it’s harder to forget the rule.
The line above the second and third slots indicates that S could go second or third (you have to move H too).
There are no added deductions you can make by placing S 2nd or 3rd, so I represented both possibilities as one scenario. The two positions are interchangeable.
The scenarios on the previous page are very rough diagrams. They are useful because they let you see how limited the game is. S can only go second, third or fourth.
I find that when I make these diagrams in advance, I see things that I wouldn’t have noticed otherwise. Many questions become very obvious, as I’ve realized the possibilities are quite limited.
I encourage you to sketch out a couple of scenarios before you start games. You may be surprised at the insights you gather. Try to split the scenarios based on an objective factor, such as “S is fourth, or S is 2/3”. Don’t just draw randomly.
I normally only draw scenarios when I can make a clear division between two exclusive possibilities. i.e. Things can only go one way, or another way.
Want a free Logic Games lesson?
Get a free sample of the Logic Games Mastery Seminar. Learn tips for going faster at logic games
Hi, I'm Graeme Blake
I run LSAT Hacks, and got a 177 on the LSAT. The single best thing I've ever made is the set of LSAT Mastery seminars. They show you how to think like a 170+ scorer when doing questions. Get them here: Mastery Seminars
I guarantee you'll like them, or you get your money back within 7 days. There's no risk. Check the reviews, people have said they improved within a few days.
---------
Photos and Updates: You can follow me on Instagram here
For updates, sign up for my email list. I update whenever I have new posts.
