oLG Game 2 Question 12 Explanation, by LSATHacksThis is a slightly unusual question. Normally, when looking for a pair where at least one has to be in, yu would look for a pair with the sufficient negated, and the necessary in. E.g. Q ➞ M
But there are no pairs like that in this game. So we’ll have to use a different method to find out what variables must be in.
The fast way to solve this question is to find a couple of working orders. If you find an order that works, you can use it to eliminate wrong answers. Any variables not included in your working order obviously don’t have to be in.
To quickly make two working scenarios, I used the main diagrams. I just started from the left and fulfilled all the sufficient conditions. Like this:
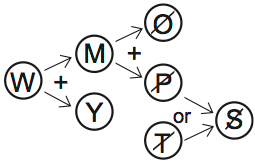
For the first diagram, that gives us WYM in, and OPST out. Add Z in to make four variables in.
Let’s make another working scenario, using the second diagram. If you activate all the sufficient conditions, SPTO are in, and MYW are out.
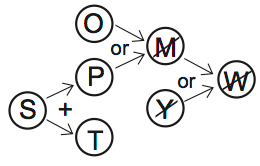
I also left Z out, because this question is asking who has to be in. Z doesn’t have to be in if we already have four variables in.
So now we have two groups of employees that fulfill all the rules:
WYMZ and SPTO
You can use these groups to eliminate answers.
A is wrong. The first group doesn’t include O or S.
C is wrong. The first group doesn’t include P and S.
E is wrong. The second group doesn’t include Y or Z.
Hopefully this method makes sense. I’m attempting to describe the kind of short cut that high scorers use routinely.
Under timed conditions, it took me all of 10 seconds to create those two groups. It takes longer to explain it, because I’m walking you through the steps I went through instantaneously in my head. I recommend practicing this question a few times to get better at quickly creating scenarios to disprove answers.
So now we’ve narrowed things down to B and D. If you use a quick method to eliminate three answers, you can afford to spend more time testing the remaining two. Let’s see if we can create a scenario without OW or without TY.
This scenario eliminates B. MYZT. It obeys all the rules, and doesn’t include O or W. For purposes of illustration, I’ll highlight all the variables I selected across both diagrams. MYTZ are in, POSW are out.
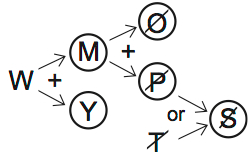
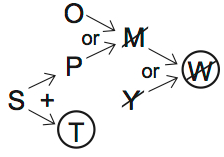
You must read the diagrams left to right. We’ve covered all seven variables across both diagrams, and none of the rules conflict.
D is CORRECT. It’s impossible to construct a correct scenario without either T or Y.
Want a free Logic Games lesson?
Get a free sample of the Logic Games Mastery Seminar. Learn tips for going faster at logic games
Hi, I'm Graeme Blake
I created LSATHacks, and scored a 177 on the LSAT.
Check out LSATHacks All Access
It's your one stop shop for LSAT prep: 1000s more explanations, and courses for both intro and advanced students. Lifetime access to everything on LSATHacks and anything I add. Plus a consult with me to get you started on the right track.
---------
Socials and Updates: If you have any questions, you can can check out my TikTok videos or email me.
For updates, sign up for my email list. I update whenever I have new posts.
Hi Graeme, thanks for all these helpful explanations! i have a question about your strategy when answering questions like these. In following along to how you answered this question, when I saw that B showed one of the two variables in both scenarios mapped out I thought you would pick B and stop there. In other answer explanations you seem to stop when you find an answer choice that fits the criteria we’re looking for to answer the question. Why did you go through all the option choices for the question? And when taking an exam do you always look at all the option choices after you’ve identified one answer that seems to work? I would imagine doing this would take up too much time. Thank you!
If you want a high score you have to look at all the answers. There are no shortcuts. I do that for every question on every section.
Keyword is look though. I just glance at the answers to make sure two don’t seem right. On many questions only one answers fits what I am looking for, so I pick that.
But I always look. The LSAT uses traps.
Hi Graeme,
Totally appreciate all of your explanations, would you mind clarifying what you mean by “if you activate all of the sufficient conditions, then ‘O would need to be in’?
As I understand it O is optional because is an optional sufficient condition, due to the “OR” and not an “AND”. So if we apply the concept that O is optional, just like Z is, then Z would have just as a logically valid a reason to be IN.
If that is the case, then the support for your reason would be less supported? However, I understand that regardless of whether O or Z is in, T and Y, MUST be in, and for this reason I would agree with D being the correct answer, that was my choice, but I am having a hard time with O and Z.
Yes, O is optional. I’m just using the diagrams to construct a couple of could be true scenarios, quickly. I’m saying use the diagram and say “I will make every sufficient condition in” and count who is in: SPTO.
Using that + the other scenario you can eliminate the wrong answers.
The reason we don’t need Z is because it isn’t in in the scenario I described. And the other scenario I described has WYMZ, which doesn’t include O.
Hope that helps!
i’ve been staring at “Normally, when looking for a pair where at least one has to be in, you would look for a pair with the sufficient negated, and the necessary in. E.g. Q ➞ M” for probably about 30 minutes now and i cannot for the life of me figure out what it means. how can a “sufficient negated” be an item in a pair?? please help!
It would mean something like: ~Q —> M
If Q is out, M is in. That means at least one of the two is always in.
Missed this when you posted but someone else may have the same question! Common difficulty