LG Game 3 Question 15 Explanation, by LSATHacks
If the final two courses are not summarized, then that means that R is not summarized, because R is one of the final two courses. We know this from our setup diagram: R is always fifth or sixth.
The contrapositive of rule 2 says that if R is not summarized, then N is summarized.
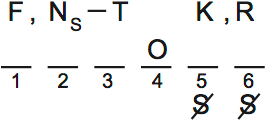
There are a few ways we could place F, N and T. The most important thing is not to make two of them summarized and beside each other. Note that T could be summarized, if you place N first.
A is wrong. K is always fifth or sixth, so on this question it can’t be summarized. C is wrong for the same reason.
B is CORRECT. This diagram shows that it’s possible for O to be summarized:
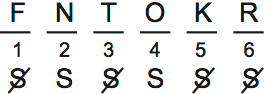
D is wrong because if F and T are summarized, then the first three courses would all be summarized. This violates the first rule.
E is wrong because if R is not summarized, then N must be summarized.
Hi, I'm Graeme Blake
Founder of LSAThacks; I scored a 177 on the LSAT.
I created the LSAT Mastery Seminars, which are part of the Ultimate LSAT Prep Bundle
If you like the explanations you're reading I'm 100% confident you'll enjoy the courses. Satisfaction guaranteed.
---------
Updates:
For updates, sign up for my email list. I update whenever I have new posts.
Hi Graeme,
Thank you so much for these explanations, they are so helpful!
For this game, I actually am having a lot of trouble understanding the contrapositive logical jump you make about Rule 2. If R or T aren’t discussed, why does that mean that N IS discussed? Is this something that’s just true and I’ll never understand why? Please help.
If we diagram Rule 2, it looks like this:
If ~N –> R and T are summarized
This diagram means that in order to NOT summarize N, you MUST summarize R and T. Remember that in order to make a contrapositive out of a conditional relationship that has an “And” in it, when you flip it, it becomes “Or”. The contrapositive looks like this:
If ~R or ~T –> N is summarized.
According to this logic, if one of R and T are not summarized, then N has to be. You can also think of it this way: in this contrapositive, N being summarized is the necessary condition. If R or T aren’t summarized, then N MUST be summarized.
A commonsense example would be like this: If you’re alive, you’re breathing, and your heart is beating.
A –> B AND HB.
So you need both.
So if one or the other is missing, you’re not alive: if you’re not breathing or your heart is not beating, you’re dead.
~B or ~HB –> ~A
This works for any statement. You reverse the terms, negate them, and switch and to or and vice versa. It’s very mechanical.
I still don’t understand why you reverse the logical statement and say that if both R and T are summarized then N is not summarized. A — > B is not always equivalent to B –> A.
Hi, I’m not sure where you see that, can you clarify?