LSAT 71, Logical Reasoning II, Q11, LSATHacks

QUESTION TEXT: Secondary school students achieve broad mastery of…

QUESTION TYPE: Sufficient Assumption

CONCLUSION: If students don’t achieve broad mastery, they aren’t being taught using appropriate methods.

REASONING: Students achieve broad mastery if they are taught with appropriate methods and they devote significant effort to their studies.

ANALYSIS: This is an unusually tricky sufficient assumption question. To get this right, you really need to draw it and see the flaw first. In fact I’m going to draw it like a logic game.

This is a long explanation. However, when I did this question myself, I did it rather quickly. The reason is that this process takes a long time to explain, but this process does not take a long time to do.

You should use this explanation to understand, but then practice the diagramming process on your own so that you learn it and can apply it quickly.

First let’s look at the conclusion. We need to get from lack of broad mastery to lack of appropriate methods:

Now let’s look at the evidence. If you have appropriate methods AND significant effort, you have broad mastery:

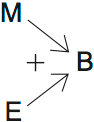
The contrapositive is that if you don’t have broad mastery, you’re missing appropriate methods or significant effort:

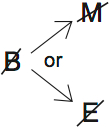
And this is where the flaw is. If we lack broad mastery, it’s possible we have appropriate methods, and the problem is that we lack significant efforts. Not good. We need to make it 100% certain that lack of broad mastery means no appropriate methods.

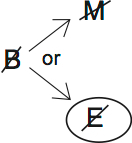
There are two possibilities when you lack broad mastery: M or E. We can guarantee the conclusion by showing that either possibility leads to M.

If we say that all appropriate methods lead to effort (M ➞ E), then this attaches on to the diagram as the contrapositive (E ➞ M):

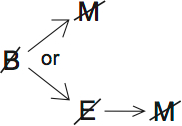
Now this matches the conclusion. If we don’t have broad mastery, then we don’t have adequate methods, no matter which path we choose.

Note: My diagrams are just one letter. If you make long, confusing acronyms, your own diagrams will destroy you. I’ve seen this happen time and time again. Diagrams are just a tool. The real knowledge should be in your head. Pick one useful letter, and remember what the letters refer to.

Note: I didn’t do this diagram the first time I did this question. I solved this question with intuition. But following these steps will help improve your conditional logic, and there will be easier questions that you can solve up front.

___________

1. CORRECT. See the explanation above. This answer matches the addition statement I added to the diagram, and proves the conclusion. If this is true, then lack of broad mastery inevitably leads to lack of adequate methods.
2. This is a reversal of part of the evidence: broad mastery ➞ significant efforts.
   We’re looking for something that tells us what happens if we don’t have broad mastery.
   The “even if” part of this answer choice is meaningless fluff, it means that appropriate methods are neither sufficient nor necessary.
3. This tells us: broad mastery ➞ appropriate methods. That’s a reversal of the evidence from the argument, where appropriate methods were part of a sufficient condition for broad mastery.
   Contrapositive of the answer: appropriate methods ➞ broad mastery.
   Not helpful. We need an answer that tells us what happens if we don’t have broad mastery. It needs to b the sufficient condition: e.g. broad mastery ➞ [something useful].
4. So? This was already implied by the stimulus. We only know that appropriate methods are a sufficient condition if they are accompanied by effort.
5. This is the same as D. We already know this is true. Efforts are only sufficient if accompanied by appropriate methods.

Recap: The question begins with “Secondary school students achieve broad mastery of”. It is a Sufficient Assumption question. To practice more Sufficient Assumption questions, have a look at the LSAT Questions by Type page.

---