LG Game 2 Setup, by LSATHacks
This is an explanation of the second logic game from Section IV of LSAT Preptest 75, the June 2015 LSAT.
Seven trees will be planted on three lots (1, 2, 3). The trees are: a hickory, a larch, a maple, an oak, a plum, a sycamore, and a walnut (H, L, M, O, P, S, W). You must determine which trees can be planted on which lot according to the rules.
Game Setup
This is a grouping game. We have to place seven trees in three lots.
From experience with similar games, it’s best to set this game up vertically:
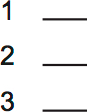
Next, read over all the rules. You shouldn’t just blindly draw the rules in order. Some rules are easier to draw than others, because they can go directly on the diagram. Draw these first.
Rules 3, 4 and 5 can go directly on the diagram:
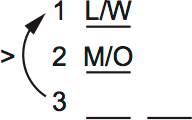
A couple notes on the symbols:
Technically, L/W and M/O are exclusive. You can’t have both. I know I’ll remember that because I’ve seen similar rules. If you aren’t certain you’ll remember, it’s best to make a separate note. Maybe “L/W” to the left of lot one, for example.
Lot three has at least two trees, because it has more than lot 1. The arrow + greater than sign is a second reminder of this rule.
This final rule is incredibly important. In every scenario you make you must check if lot three has more than lot one. And in some cases, the final rule determines the distribution.
For example, some questions place exactly three trees in lot two. This means that lot 1 has one tree and lot 3 has three trees – that’s the only way to divide the trees between those two lots and still obey the final rule.
The other two rules can’t be drawn directly, so you should put them in a numbered list:
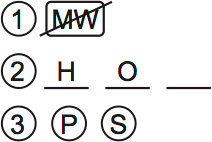
The circled P and S means that those two variables have no rules. The “H O __” means that the hickory and the oak are in a lot together with one other tree.
I couldn’t make any deductions that I could draw. However, it’s important to consider numerical distributions.
We have seven trees. At least one is in lot 2. That leaves six trees to divide between lot 1 and 3. And lot 3 needs more than lot 1.
That means we can’t put three trees in lot 1, because then there would only be three trees to put in lot 3.
So lot one has, at most, two trees. I didn’t write this down because it’s fairly straightforward if you remember the final rule. But it you sometimes make mistakes with numerical distributions, you should write this deduction down.
Likewise, it’s important to consider where you could place the hickory, oak and 3rd tree (rule one). They could only go in lots 2 or 3, because lot 1 can’t have three trees.
Hi there, thank you for your helpful explanations. Can you please explain how we can infer that lot 3 does not have more than 3 trees? Couldn’t it have 4 or even 5? What about Lot 2? Couldn’t it have 4 trees, which leaves 2 for Lot 3 and we would not break rule 5?
Thank you.
Because of rule 1. One of the lots has: hickory, oak, one other. Three trees. And lot one has at least one tree.
So either:
1. Lot 3 has hickory, oak, one other. –> Lot 3 has three trees
2. Lot 2 has hickory, oak, one other –> There are only four trees left. And lot 1 has one of them, leaving 3 trees for lot 3.
The key to rule 1 is it is describing the full list of trees at that lot.
Why is it that it has seemingly been assumed that no lots can have zero trees? I see in the setup it says, “Each tree must be planted on EXACTLY one of three lots.” I suspect is with the logic based verbiage of the word “exactly”, but if it’s not, the colloquial interpretation of that sentence would just be that each tree can only be planted on one lot, not that each lot must have at least one tree. And I didn’t see anywhere else that made that stipulation. Thank you for any help!