LG Game 3 Question 17 Explanation, by LSATHacks
This question places R alone. That means the group structure will be 1-2-3. R alone, two others in markets, and three in a third group. Like this:
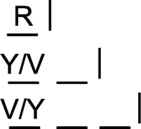
I’m purposefully leaving off the group labels, because I want you to think about how to separate the assistants into the three groups. For example, Y/V are split between the two other groups, because rule 3 says they can’t be together.
Next, TS is hardest to place. Needs two spaces. So, TS must go in the group of three:
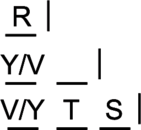
That leaves only Z left to place, and only one spot open:
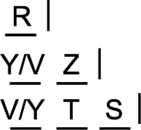
So we have figured out the entire distribution of assistants between the 1-2-3 groups! And guess what, that solves the question. We know that the group of two is Markets (rule 1). So, we know for sure that Z is in markets. D is CORRECT.
You could also have gotten the right answer by making diagrams figuring out which of the groups above go in L, M and P. But it would have taken longer. And on logic games you should always learn the fastest method.
(Adding in the three groups would have complicated things by forcing you to think about whether YZ were in P together, for example.)
Please help me.
Why can’t E be correct… Why isn’t it necessary that S + T go in Pricing. If they go in M they force Y and Z into pricing and violate the rule that says Y can’t go with V.
Please help. I feel like my logic circuit is breaking and I don’t know what to do.
There are two possible setups for this question. They look like this:
Diagram 1
L M P
R Y S
Z T
V
Diagram 2
L M P
S Y/V R
T Z
Y/V
While in Diagram 1, ST have to go in Pricing, because otherwise Y and V would be forced together. But that isn’t true for Diagram 2. In Diagram 2, R occupies Pricing and is the only assistant assigned (as per the question’s instuctions). Because Rule 3 says that Y and V can’t be assigneed together, we know that one of them will go in L and one will go in M. ST must go together so they must both be assigned to L in this case. Thus, in both diagrams, Z being assigned to M is the only constant, making D the correct answer.
I don’t understand why the answer isn’t E. I don’t see where Smith could go besides pricing. In the diagram you have V/Y in pricing, but if Y was there, then Z would have to be. So pricing has to be: VTS