LG Game 2 Question 9 Explanation, by LSATHacks
This is a counting question. Look at both diagrams, and see how many birds can be in.
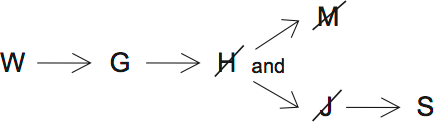
If W is in, then W, G, and S are in. That’s 3 birds.
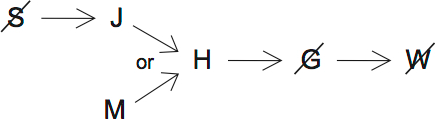
On this diagram, S, J, M and H are can be in. That’s 4. C is CORRECT.
Yes, you read that right. S can be in. Here’s how.
Start with J in. Don’t start with S out – you’re trying to put birds in!
If J is in, H is in. You can also put M in. J, M and H make three.
Only S is left. You don’t know anything about S if you start with J. Remember, you can only read the diagram left to right.
You can also put S in. Both S and J can be in together. S, J, M and H make four.
Review the setup if you’re not sure why S and J can both be in.
This makes no sense to me – it says that if J is not in, then S is. To me, it doesn’t matter how the diagram reads, maybe I’m taking this all too literally. I’m just seeing this as black-and-white. I’m still super confused.
Can you elaborate? You’ve stated it correctly. If J is not in, then S is. Do you mean to say you think that is false, or were you unsure about another point?
Sorry, I was writing this at a time when I was going through total brain fog. I meant to ask, how can S be in when J is also in? The rule says if J is not in, then S is. So why do we have both here? Why is that allowable?
I would have never thought that we could put both together, by looking at the fourth rule alone. Could you dumb this down for me at all? Lol
“ You don’t know anything about S if you start with J” this is confusing me even more, how could you assume this? I feel like this line is throwing me off.
Ok let’s say we have two parents. At least one of them will pick up their child from daycare.
If mom doesn’t go –> dad goes
If dad doesn’t go –> mom will
The idea here is that someone will be there for the kid. Use common sense: both can go two right? The idea of such a rule is to ensure at least one will go, *and maybe both*
Same thing with not S –> J, and not J –> S
It’s an “at least one, maybe both” rule.
If you want to think formally, remember you can only move from left to right. So, if you start at J in, there is nothing to the right of it, so you can conclude nothing.
Does that make sense?
OHHHH!!! Light bulb moment. So let’s say instead it says something like “If S is in the forest, J cannot be in the forest at the same time”, then we’d know FOR SURE that there cannot be both birds at the same time?
But because the rule is kind of ambiguous in that sense, it kind of leaves the door open to the possibility that both could be in, if they wanted to?
Thanks :)
>OHHHH!!! Light bulb moment. So let’s say instead it says something like “If S is in the forest, J cannot be in the forest at the same time”, then we’d know FOR SURE that there cannot be both birds at the same time?
Yeah, exactly! And for the other form, it isn’t that it’s ambiguous. It’s that it’s saying a different thing.
Like if you go to a bar and order something, you *need* to order either food or a drink. Or else they’ll kick you out. So no food –> drink, and no drink –> food
If you lack one, you must get the other. But you COULD get both. The bar would be very happy if you ordered both. No ambiguity.
So one form is: At least one out, and maybe both out
And the other is: at least one in, and maybe both in
Why can’t all six be in? If S were in, that would fail the sufficient and make everything downstream technically irrelevant. It wouldn’t be triggered. I know that I am wrong; however, I would like to understand when a sufficient or necessary failing means that other relationships do not matter versus when other relationships continue to apply. Thank you so much.
You can refer back to the setup page for a more comprehensive explanation. If S were in, it would not make everything downstream irrelevant because of the way it is related to J. The relationship says that if J isn’t in, then S is. This means that S is required for J to not be in. So it isnt’ the case that they can’t be in together, but that for J to be allowed to be out, S has to be there.
So we can have 3 cases: J and S both in, J in and S out, and S in and J out. So in this case, S doesn’t trigger anything, but elements down the rest of the chain would trigger for some to be out. For example, if J is in, then Rule 2 states that H must be in. Rule 1 and Rule 3 together then say that G and and W would then be out.
I am so confused with question 9. I understand the logic this explanation uses to illustrate how if G and W are out then H, J, M, and S can be in. With that logic, if H, J, M are in, then any sufficient conditions could also be in, (in this case also S), and therefore count a total of 4 in. But with this logic of making all sufficient conditions free floaters, couldn’t you also do the following to justify there being 6 in the “in” category?
/S —> J —> H –> /G —> /W
……..M –>
(and then run the contrapositive)
W —> G —> /H —> /J —> S
…………………..—> /M
In this case, all you could say is S is in, and therefore, let all other letters be sufficient conditions, and therefore free floaters, and therefore put them all in the “in” category, and therefore count a total of 6 as “in”.
How could this alternative possibility not be wrong?!?!?!?!?!?!?