LG Game 4 Setup, by LSATHacks
This is an explanation of the fourth logic game from Section II of LSAT Preptest 74, the December 2014 LSAT.
At least two photographers will be assigned to each of two graduation ceremonies. The graduation ceremonies will be held at Silva and Thorne University (S, T). The six photographers are Frost, Gonzalez, Heideck, Knutson, Lai, and Mays (F, G, H, K, L, M). The rules allow you to determine the possible assignments of the photographers.
Game Setup
This game can be divided into two scenarios that greatly simplify the game. This is a common trend on modern logic games, so be sure you understand this setup.
I recommend drawing the diagrams on a sheet of paper yourself in order to follow along. Ideally, print a fresh copy of the game to use.
In this game, there are two groups: Silva and Thorne. Each group needs at least two photographers:
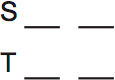
FH go together:
Technically this is a linear diagram, but it works just as well for grouping. Using the same symbols in both cases makes for simpler diagrams.
Next, L and M can’t go together:
Next, if G is in S, then L is in T:
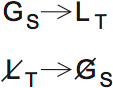
I drew the diagram and its contrapositive in this explanation. On my own sheet, I didn’t draw the contrapositive because I can do it in my head. When you are still learning contrapositives, draw them, but aim to be able to instantly see them in your head.
The next rule is complicated. It says that if K isn’t assigned to T, then H and M must both go in T.
We could leave it at that, but both H and M were mentioned in other rules. F is with H, and L can’t go with M. So the full effect of the rule is this:
There’s still more. If something complicated happens when a rule occurs, follow the idea as far as it goes. It’s best to draw the scenario.
Lets do that. If K isn’t with T, then F, H and M are there:
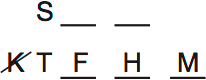
We also know that L isn’t with T, because M is there (rule 2). This affects rule 3: G can’t go with S.
There’s till more. S needs at least two photographers. FHM are already at T. G can’t go to S. So only L and K are left, and they must go to S:
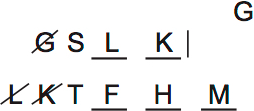
Only G is left uncertain. They could go to T, or they could not be assigned. (Not all photographers have to go somewhere).
So if K isn’t assigned to T, then we know almost everything. The scenario above is the only possible scenario.
Therefore, in all other scenarios, K is assigned to T:
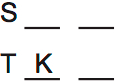
Drawing K there may not seem like a major deduction, but this has two big effects.
- We no longer have to remember the fourth rule. This significantly reduces the difficulty of working with the remaining rules.
- The deduction about K solves question 18 completely, and largely solves 19, 20, and 21.
There are big payoffs for seeing if a game can be split into two scenarios.
Want a free Logic Games lesson?
Get a free sample of the Logic Games Mastery Seminar. Learn tips for going faster at logic games
Hi, I'm Graeme Blake
I created LSATHacks, and scored a 177 on the LSAT.
Book a free consult with me to discuss how you can improve your score: Book a consult
---------
Photos and Updates: If you have a question, you can follow us on Instagram here or send an email.
For updates, sign up for my email list. I update whenever I have new posts.4
How do you know that K has to be placed?
Let’s look at the two diagrams separately. In the first diagram, where FH are assigned to T, the contrapositive of Rule F says that if M and FH are assigned to T, then K cannot be assigned to T. So, the options for K here are to either be assigned to S or not assigned. However, Rule 2 then says that L and M can’t be assigned together, so L has to be assigned to S. Rule 3 says that G can’t be with S (since L isn’t with T). The stimulus tells us that there has to be at least 2 photographers assigned to each school. FHM are at T already so they can’t go to S. G also can’t go to S. L and K MUST go to S. So, in this case, K has to be placed.
In the second diagram, K has to be assigned to T so that there can be more scenarios in addition to the aforementioned. Why? Because not placing K would be the same as not placing K with T and would give the same effects. So, in order to explore the alternative scenarios, K must go with S.
FH is mandatory based on Rule 1 and confirmed by Q20: Rule 1 states “F must be assigned together with H to one of the graduation ceremonies.” Q20 provides a MBT inference check – and every answer choice contains F and H.
For me, I mostly agree but will try four frames if two “big” rules (2 rules x 2 rules = 4 frames) can be pushed together. In addition to revealing inferences, this simplifies the game by “eliminating” two rules that after the first question I’ll never have to check again, and saves time on the backside by quickly necking down possibilities for some local “If/then” and most global “Which of the following” Qs. That said, I agree that more than four frames risks wasting time due cluttered confusion and hypotheticals that don’t play out.
Btw, thanks for the response and, especially, all the outstanding explanations – so clear and spot-on.
Yes, thanks for catching that part of the rule re: F and H. F and H must be placed. The explanation will be updated to reflect that.
As for the templates, I also tend to limit the templates I draw to two–unless I have three very complete templates. I draw in the other possibilities as I do questions. I’ve found that any time that I save up-front by drawing out more than 3 templates is usually lost when I have to revisit every one of the 4+ templates to answer questions.
That being said, I have seen a couple students be very successful at games by going beyond 2-3 templates, so I don’t rule it out as an approach.
Rules clarification: the FH block MUST be placed into one or the other (i.e., cannot be out). Recommend further splitting based on mandatory placement of FH block. Combined with placement of K (as outlined by Graeme) this maps out all frames and makes the game even faster.
Maybe I missed something: why do you say FH have to be placed? You could have this:
S: G M
T: K L
So if you split on FH, you’d need to draw two scenarios for that + the scenario I drew in the explanation + the one in this comment. For me, personally, I find splitting into four scenarios too many, as it’s easier to create them as needed for questions.
Hi Graeme,
This comment confuses me. The rule says that F and H must be assigned together to one of the graduation ceremonies. Therefore, I don’t understand how this scenario would work. Because I saw that rule, I immediately thought to divide the game based on FH in S or FH in T. Why did you choose to split based on K rather than FH?
Splitting based on K would be simpler and only yield 2 diagrams. Splitting by FH would result in 3 diagrams. This is because of Rule 4, which says:
~KT –> HT and MT
The contrapositive would be: it ~HT or ~MT –> KT
Based on this conditional relationship, splitting by K ony results in 2 scenarios:
1) If K is assigned to S (~KT), then you know that FHM have to be assigned to T, which leaves L to be assigned to S and G to either be assigned to T or not assigned.
2) K is assigned to T, then FH would have to be assigned to S. Then G, L, M could or could not be assigned.
This is a lot simpler than if you split by FH, which gives 3 scenarios (due to and/or):
1) FH assigned to S and K assigned to T.
2) FH assigned to T and K assigned to S.
FH assigned to T and K also assigned to T (this is possible as long as M is not assigned to T).
What initially tipped you off that you could make this into 2 scenarios?
Good question. Because there was a conditional rule. Often, if games give a single sufficient condition, you can find two scenarios by making one where the condition occurs, and one where it doesn’t.
In this case, the initial condition is “K not in T”